
(original size image)
As of January 2004 au.riversinfo.org is archived under Precision Info
RIVERSINFO AUSTRALIA ARCHIVE
This archive provides non stylised versions of selected reference documents (formerly) resident on au.riversinfo.org.
Final Report Project E6 National River Health Program
Water Services Association of Australia Melbourne Australia
John Parslow, John Hunter, Adam Davidson.
CSIRO Marine Research. Hobart, Tasmania
Foreword & Publication Details
Executive Summary & Acknowledgements
3. Biogeochemical Process Models
4. Analysis of a Steady-State 1-Box Model
5. Simple Inverse Models for Driving Estuarine Transport and Eutrophication Models
6. Application of a Simple Spatially-Resolved Eutrophication Model
This report describes the outcomes of a research project conducted under the Urban Research and Development sub-program of the National River Health Program (NRHP).
The NRHP is an on-going national program established in 1993, managed by the Land and Water Resources Research and Development Corporation (LWRRDC) and Environment Australia. Its mission is to improve the management of Australia's rivers and floodplains for their long-term health and ecological sustainability, through the following goals:
Urban streams and estuaries (i.e. those affected by runoff and discharges from urban areas) are an important subset of Australia's waterways. Most are degraded biologically, physically and chemically and therefore require appropriate methods to be developed for health assessment and management. The Urban R&D Sub-program, managed by the Water Services Association of Australia, comprises 8 research projects which were developed to meet research priorities for urban streams and estuaries within the goals of the NRHP and to complement existing NRHP projects on non-urban rivers. Thus, research focuses on development of standardised methods for assessing the ecological health of urban streams and estuaries which can be linked with data on water and sediment quality. The urban R&D projects commenced in 1996.
The definition of health in urban waterways used is "the ability to support and maintain a balanced, integrative, adaptive community of organisms having a species composition, diversity and functional organisation as comparable as practicable to that of natural habitats of the region".
The eight projects of the Urban Sub-Program are:
| Decision support system for management of urban streams | Dr John Anderson Southern Cross University, Lismore |
| RIVPACS (River InVertebrate Prediction and Classification System) for urban streams | Dr Peter Breen CRC for Freshwater Ecology, Monash University, Melbourne |
| DIPACS (Diatom Prediction and Classification System) for urban streams | Dr Jacob John
Curtin University, Perth |
| Sediment chemistry- macroinvertebrate fauna relationships in urban streams | Dr Nick O'Connor Water EcoScience, Melbourne |
| Classification of estuaries | Dr Peter Saenger Southern Cross University,Lismore |
| Literature review of ecological health assessment in estuaries | Mr David Deeley
Murdoch University, Perth |
| Estuarine health assessment using benthic macrofauna | Dr Gary Poore
Museum of Victoria, Melbourne |
| Estuarine eutrophication models | Dr John Parslow CSIRO Marine Laboratories, Hobart |
Published by:
Land and Water Resources Research and Development Corporation
GPO Box 2182 Canberra ACT 2601
Telephone: (02) 6257 3379
Facsimile: (02) 6257 3420
Email: public@Iwwrrdc.gov.au
WebSite: www.lwrrdc.gov.au
© LWRRDC
Published Electronically on au.riversinfo.org by the Environmental Information Association (Incorporated) with the permission of LWRRDC and Environment Australia. Environment Australia assisted by providing copies of the manuscript for electronic publication. The Natural Heritage Trust provided project funds which were used to assist in publishing this material. In the case of variation between this document and the hard copy original the original takes precedence. (Bryan Hall).
Disclaimer:
The information contained in this publication has been published by
LWRRDC to assist public knowledge and discussion and to help improve the
sustainable management of land, water and vegetation. Where technical information
has been prepared by or contributed by authors external to the Corporation,
readers should contact the author(s), and conduct their own enquiries,
before making use of that information.
Publication data:
Estuarine Eutrophication Models Final Report Project E6 National River Health Program Water Services Association of Australia Melbourne Australia John Parslow, John Hunter, Adam Davidson. CSIRO Marine Research. Hobart, Tasmania
Report No 12, LWRRDC Occasional Paper 19/99.
ISSN 1320-0992
ISBN 0 642 26769 3
Managing Agencies
Increased human development in the coastal zone leads to increased nutrient loads to estuaries and coastal waters both through changes in catchments and river runoff, and point source discharges to estuaries. Eutrophication (ie the response of ecosystems to these increased nutrient inputs) is recognised as a major environmental problem, both nationally and internationally.
This study has been undertaken "to develop and demonstrate a widely applicable model of eutrophication processes in urban estuaries which can predict the potential for phytoplankton blooms and bloom type on the basis of environmental data". Existing estuarine eutrophication models range from simple load-response relationships to complex "realistic" process-based simulation models. After reviewing these models in Sections 1 to 3, we focus on the development of relatively simple process-based models, which incorporate the core variables and processes controlling the cycling of nutrients and bloom development in estuaries. Models of this kind offer advantages over load-response models in dealing with the wide range of physical environmental conditions in estuaries, and offer advantages over more complex models in reduced data requirements, lower implementation costs, and amenability to analysis and understanding.
The core state variable description used here describes nitrogen cycling and algal biomass in terms of 4 pools: phytoplankton N, dissolved inorganic N (DIN), labile organic N and refractory organic N. The core processes include phytoplankton uptake and growth (dependent on light and nutrient levels), phytoplankton mortality, production and breakdown of labile and refractory organic N, and sediment respiration and denitrification. This core biogeochemical process model is implemented in two physical contexts: a steady-state one-box model, and a dynamical spatially-resolved model.
We present an analysis of the behaviour of the one-box steady-state model in response to changes in external loads, and compare this with simple load-response models developed for lakes. By analogy with the load-response models, the model defines two kinds of relationships involving total nitrogen (TN):
The relationship between TN load and TN pool in estuaries is controlled by a combination of physical exchange with the ocean, and the magnitude of internal sinks. In the absence of an internal sink, the steady-state TN pool is equal to load multiplied by flushing time. In the models discussed here, the principal internal sink for nitrogen is denitrification. In estuaries with long flushing times (order 100 days), denitrification may account for more than 80% of the nitrogen load, and maintain the estuary in a mesotrophic condition under loads which, in the absence of denitrification, would create eutrophic blooms. In estuaries with short flushing times, of order 10 days, export dominates over denitrification, and there is no critical transition in water quality with increasing load.
In estuaries with long flushing times, increases in loads lead to increases in the production and remineralization of organic matter in both water column and sediment. Sufficient increases in load and sediment respiration rates can shut down sediment denitrification (Murray and Parslow, 1997), leading to a "catastrophic" transition from mesotrophic to eutrophic status. Results from Port Phillip Bay suggest a critical nitrogen load (denitrification capacity) of about 30 mg N m-2 d-1. Coastal lagoons with restricted or intermittently open entrances are likely to be especially vulnerable to denitrification failure.
Phytoplankton utilisation of DIN is controlled by light attenuation and depth. In estuaries with low background attenuation, increasing loads of DIN will lead to increased phytoplankton biomass, until phytoplankton biomass is limited due to self-shading at high levels (order 20 to 50 mg Chl a m-3). Further increases in load result in accumulation of DIN. In deep estuaries which have high light attenuation due either to suspended solids or gelbstoff, light limitation can limit maximum phytoplankton biomass to quite low levels (order 2 to 5 mg Chl a m-3), and excess DIN will accumulate even at low loads.
Most estuaries contain high levels of refractory organic N derived both from the catchment and from exchange with coastal marine waters. At low to moderate loads of available N (oligotrophic to mesotrophic conditions), this refractory N dominates the TN pool and mass balance in estuaries.
For many estuaries with long-estuary salinity gradients, the one-box model with its single flushing time is simply not valid, and a spatially-resolved model is required. In this study, we use a spatially resolved model (the Simple Estuarine Eutrophication Model, or SEEM) based upon an n-layer hybrid inverse model. This approach can be regarded as an extension of more traditional methods which use the salinity distribution to infer flushing rates.
A key limitation of the inverse model is the assumption of steady-state flow and exchanges. This is reasonable provided river flow changes on time scales which are not too short compared with flushing times. Many Australian estuaries are subject to long periods of low flow, with intermittent flood events. The steady-state assumption works quite well during the low-flow periods, but is likely to fail during brief flood events. In those urban estuaries where point source loads are the major cause of eutrophication, water quality problems are most apparent during low-flow periods. Where diffuse loads dominate, or the interaction between diffuse and point source loads is thought to be critical, more sophisticated dynamical models may be required.
The spatially resolved biogeochemical model has been applied at steady state to three test cases: the Derwent, Brunswick and Hardy estuaries. These represent contrasting physical environments in terms of morphology, runoff and stratification. The Derwent is a deep, strongly-stratified estuary, with high river runoff and high light limitation due to humics. The Brunswick is a shallow, tidally-dominated, turbid estuary, while Hardy Inlet represents a broad shallow lagoon connected to the sea by a deep channel. Both the Brunswick and Hardy receive very low river runoff for long periods.
Model and data analysis suggest that phytoplankton biomass in the Derwent is primarily light-limited, especially in winter, when DIN levels are high due both to point source loads and elevated nitrate concentrations on the adjacent continental shelf. In the Brunswick, point sources loads are dominant during periods of low river flow, while the Hardy receives diffuse catchment loads. Both the Brunswick and Hardy appear to operate as P-limited systems, and the N-limited model was successfully adapted as a P-limited model for these systems. While light attenuation coefficients are much higher in the Brunswick than in the Derwent, the Brunswick is much shallower and supports higher phytoplankton biomass.
The use of the inverse transport model allows us to budget total N and P, and to identify internal sinks of N or P which are not represented by the model. However, this is made more difficult by the presence in all three estuaries of high levels of organic N and P, presumably refractory, which tend to dominate the mass balance, especially in the case of N. The problem is that internal sinks may be an appreciable part of the "available" N budget, but a small part of the total N budget.
Model experiments with the Derwent and Brunswick test cases highlight the importance of the location of point source discharges within the estuary. Effective flushing rates can vary by more than an order of magnitude along estuary. In the case of the Derwent, shifting an outfall by 10 km in the mid-estuary has a major impact on resulting water quality. In strongly stratified salt-wedge estuaries, the two-layer circulation, combined with sinking of detritus, can act to trap nutrients in the estuary, and discharging effluent into bottom waters can greatly increase residence time and water quality impacts.
The SEEM model has been calibrated using test case data collected on more or less "routine" environmental surveys. These surveys comprised from 5 to 20 stations, sufficient to resolve the long-estuary salinity gradient. Samples were taken in top and bottom layers in stratified estuaries. The minimum standard water quality measurements required by the model are Chl a, DIN, DIP, organic N (TKN), organic P and secchi depth. The model requires river flow and diffuse and point source loads (as DIN, organic N, DIP, organic P) at the time of surveys. The model calibration and analysis underscores the need to develop operational methods to distinguish labile and refractory organic N and P in field surveys.
The SEEM model has been developed in JAVA, with a graphical user interface providing run management and graphical displays of output results. It has been designed so that implementation and application to new estuaries can be undertaken quickly. It is our intention to apply it to a broad range of test cases as data become available.
A high priority for further development is the implementation of a robust statistically rigorous parameter estimation framework around the model. Bayesian techniques, such as the Monte Carlo Markov Chain method, would allow the user to establish prior probability distributions for the parameters, and characterise their joint posterior probability distribution. These methods can be used not only to quantify the uncertainty in management predictions, but also to quantitatively assess the information content provided by alternative field measurement programs.
This study was supported by the Water Services Association of Australia, under the National River Health Program. The authors gratefully acknowledge Christine Coughanowr, Bradley Eyre and David Deeley who provided test data sets. The authors would also like to acknowledge the valuable contributions of Graham Harris, Sandy Murray, Peter Thompson, Sue Blackburn and Stephen Walker through collaboration and discussion.
The term eutrophication is used generally to refer to the response of ecosystems to increases in nutrient loads. In many natural systems, primary production and community biomass and composition are thought to be limited or controlled by rates of nutrient supply. Systems which are severely nutrient limited are described as oligotrophic. As nutrient supply increases, systems are successively described as mesotrophic, eutrophic and hypertrophic. A quantitative definition of these classes in terms of areal rates of primary production has been proposed by Nixon (1995). Gray (1992) provides a description of the effects or symptoms of marine eutrophication as evident in macroalgae, phytoplankton, benthic communities and fish. Gray argues that small increases in nutrient supply can result in an increase in production without serious modification of community composition (the enrichment phase), but further increases in nutrient loads result in more serious impacts on water and sediment quality and community composition and function, leading ultimately to anoxia and loss of most taxa.
It should be emphasized that natural marine systems cover the span from oligotrophic (eg the subtropical gyres and coastal seas) to mesotrophic (temperate coastal waters) to eutrophic (upwelling systems). Natural processes can also produce increases in nutrient loads on a range of time scales. However, eutrophication is widely used to refer to the effects of anthropogenic increases in nutrient loads. In this sense, eutrophication is widely recognised as one of the most important environmental issues for coastal marine systems, both internationally (eg GESAMP, 1990, Richardson and Jorgensen, 1996) and nationally.
It is hardly surprising that eutrophication is an important environmental issue. Both in Australia and internationally, human population growth and development is concentrated in the coastal zone, and has led directly to large increases in nutrient loads into estuaries, coastal embayments and coastal seas. These loads occur at population centres through direct point source inputs (eg from wastewater treatment plants and industrial outfalls). They also occur as increased diffuse catchment loads resulting from widespread modification of catchments, and intensive agricultural development and use of fertilizers.
Environmental managers dealing with eutrophication are faced with difficult choices. Reducing wastewater nutrient loads from large cities can require infrastructure investment amounting to many hundreds of millions of dollars. Reductions in loads from catchments may require extensive changes to land use practices, and/or investment in infrastructure (eg development of artificial wetlands) in streams, with uncertain outcomes. These financial and opportunity costs are ultimately borne by the general community, or particular sectors of the community.
Management decisions should be based on appropriate information. Managers require an assessment of the current state of the ecosystem, and how this has changed over time. Where there is evidence of unacceptable environmental impact, managers need an attribution of cause and effect. Is degradation caused by nutrient loads, and if so, is it due to specific point source or diffuse loads? Perhaps most importantly, managers need predictions about the likely response of the ecosystem to alternative management actions, including increasing or decreasing nutrient loads from specific sources. Predictions of this kind can be incorporated into informal or formal decision analysis procedures, addressing tradeoffs between environmental and other values or costs (Holling, 1978).
The predictions needed by managers are all based on models, in the broad sense of the term. These may be simple heuristic models, based on accumulated experience, or complex process-based simulation models. In fact, scientific understanding and modelling of eutrophication are arguably well-developed, compared with other marine ecological issues. Eutrophication is an important and obvious environmental problem, and has attracted much applied research. More generally, marine biogeochemistry has been a major focus of scientific research, and this attention has increased recently due to concern about global biogeochemical cycles, and the carbon cycle in particular (Evans and Fasham, 1993; Gordon et al, 1996). Some of the key processes in eutrophication (eg nutrient and light limitation of phytoplankton growth) are among the best studied and understood of ecological processes (eg Falkowski and Woodhead, 1992) However, while eutrophication may be comparatively well-studied, there are still questions, gaps and surprises in eutrophication modelling and prediction.
Models of eutrophication can be divided roughly into two classes: simple load-response models, due to Vollenweider (1975) and subsequent authors, and process models, which address the underlying physical, chemical and biological processes.
The load-response models were originally developed and applied to phosphorus limitation in temperate northern hemisphere lakes (Vollenweider, 1975; Schindler, 1978). While these are often referred to as empirical models, they are, as we discuss in Chapter 2, based on an elegant and careful abstraction of a few key processes. It is generally agreed that understanding and prediction of eutrophication is better for lakes than for estuaries, partly because limnologists have the advantage of many more replicate studies. Even so, attempts to extend the load-response models to a wider variety of lakes have encountered significant problems (eg Smith and Shapiro, 1981). There have also been attempts to extend this approach to estuaries (Monbet, 1992). In general, estuaries are more complex than lakes, both physically and biogeochemically, and it is not at all clear that the approximations implicit in the load response models are appropriate.
Over the last decade or so, the rapid increase in computing power, combined with increased process understanding, has seen an explosion in the development of process-based models of nutrient cycling and eutrophication in estuaries and coastal waters. International research programs such as JGOFS and LOICZ have also contributed strongly to model development (Evans and Fasham, 1993; Gordon et al, 1996). These process-based models generally have core processes and variables in common, but vary in detail. Some are based on high-resolution, realistic physical models, while others are based on simple 1-box or vertical column models. Some incorporate many trophic levels and large numbers of functional groups at each trophic level, while others deal only with nutrient and phytoplankton.
In Australia, the 1990s have seen a series of large studies of environmental impacts of nutrient loads in coastal waters in Perth, Sydney, Melbourne, Brisbane. Each of these studies has included a significant program of model development, and these models have contributed significantly to both scientific understanding and management decision-making. It is fair to say that scientific understanding is at a point where a substantial investment in eutrophication model development by competent scientists can be expected to yield useful results for managers.
That said, there are still compelling reasons to look carefully at the relationship between simple semi-empirical models and complex process models. Complex models still tend to be developed independently in individual studies, and modified to fit local interests and results. These models are often used to make predictions about the effects of changing loads outside the range of observed loads, and their reliability under these conditions is not well understood. More generally, it is not clear what level of model complexity yields the most accurate or reliable predictions for managers. It is generally thought that models with intermediate levels of complexity perform best, but there have been few studies which have attempted an objective assessment (eg Costanza and Sklar, 1985). Certainly, the number of parameters and computational load in complex realistic models have to date precluded formal approaches to parameter estimation and model identification, and model calibration has generally remained a heuristic process.
In the Port Phillip Bay Environmental Study, Murray and Parslow (1997) showed that simple process models derived by careful approximation can capture the key dynamical feedbacks in a complex simulation model, and contribute significantly both to parameter estimation and system understanding. Such simplified models offer the potential for application of new sophisticated statistical approaches to parameter estimation (eg Harmon and Challenor, 1997).
Finally, while the major metropolitan centres may be able to afford significant investments in large environmental studies and associated model development, smaller regional centres must deal with significant eutrophication problems with smaller resources. There is an important role for simpler models which can be implemented quickly, with minimal data requirements, to provide useful management support. The cost of the field surveys and process studies needed to calibrate complex models may represent more of a constraint than model implementation itself, especially as improvements in support tools and user interfaces reduce the time and resources needed to implement more sophisticated models.
This study has focused on the development and analysis of simple robust models which can be used in situations where a large investment in surveys, process studies and model development is not practical. The formal objectives of the study have been "to develop and demonstrate a widely applicable model of eutrophication processes in urban estuaries which can predict the potential for phytoplankton blooms and bloom type on the basis of environmental data".
As Gray (1992) points out, the impacts of eutrophication extend well beyond phytoplankton to affect benthic communities and higher trophic levels. We can roughly separate impacts into changes in water and sediment quality (nutrient concentrations, phytoplankton biomass, turbidity, dissolved oxygen) and ecological impacts (benthic plants and fauna, plankton composition, fish communities). The former are well-addressed by biogeochemical models, while the latter are still primarily addressed qualitatively, using comparative studies.
This study deals with the biogeochemical aspects of eutrophication, and the prediction of phytoplankton biomass in particular. We address the issue of bloom composition qualitatively in Chapter 7, but the report does not attempt to address the problem of setting water quality criteria to protect particular ecosystems or communities.
The report is structured as follows. Chapter 2 briefly reviews the classical load-response models and their application to estuarine systems. Chapter 3 reviews process-based eutrophication models, and proposes a core biogeochemical description which forms the foundation of the simple models used here. Chapter 4 presents results obtained using the simplified biogeochemical model in a 1-box, steady-state framework, which allows direct comparison with the load-response models. Chapter 5 addresses physical transport in estuaries, and presents a simple robust inverse modelling approach to quantifying horizontal and vertical physical exchanges in estuaries. This is used as a basis for a spatially-resolved biogeochemical model, and Chapter 6 presents a set of case study applications of the spatially-resolved model. Chapter 7 discusses the prediction of algal bloom composition, and its implications for eutrophication modelling. Chapter 8 provides a general discussion and conclusions. Detailed documentation of the spatially-resolved model is presented in a separate publication (Parslow et al, 1999).
Load-response models were originally developed by Vollenweider (1975), Schindler (1978) and others to describe temperate northern hemisphere lakes. They are designed to predict mean chlorophyll levels from phosphorus load. They include empirical constants, and have the advantage of having been calibrated against a large number of lakes encompassing a wide range of nutrient loads and chlorophyll concentrations. However, these are not simply black box empirical models.
These models treat lakes as well-mixed boxes, with a flushing time t
defined by the ratio of the lake volume V (m3) to the volume flux through the lake, R (m3 d-1). The flushing rate r
= R/V (d-1) is just the inverse of t
. If we consider a conservative tracer with concentration M, the load LM into the lake must be balanced by the export from the lake, R.M:
| LM = R.M. | 2.1 |
If LM = LM/V is the load per unit volume, then it follows that:
| LM = r.M. | 2.2 |
The total phosphorus concentration in the lake, TP, might be expected to be approximately conservative. Phosphorus may be subject to a wide range of transformations within the water column (eg assimilation by phytoplankton into organic matter, consumption and remineralization by zooplankton and bacteria, adsorption onto inorganic suspended sediment), but these will not change TP. However, there is an internal sink S of TP within lakes due to burial of adsorbed P or organic P in the sediments. Mass balance then gives:
| LP = R.TP + S | 2.3 |
In order to predict TP, we need to know how S is related to load or TP. Based on analysis of a large number of lakes, Vollenweider (1975) found that the sink S per unit area is proportional to TP, with a constant of proportionality which is independent of load, or lake geometry and flushing rate. This constant w has units of velocity, and is typically about 10 m y-1. If A is lake area, we can then write:
| LP = R.TP + w .TP.A | 2.4 |
| TP = LP/(R + w .A) | 2.5 |
Dividing by volume V, we get:
| TP = LP / (r + w /D) | 2.6 |
where D is the mean depth.
Even setting aside the empirically derived dependence of the internal sink on depth, this formula incorporates the mass-balance effects of load, lake volume and flushing time on total phosphorus concentration.
While TP is a logical choice for mass-balance, it is not necessarily a useful indicator of water quality. The model has been extended using a direct empirical relationship between chlorophyll a and TP. Early results showed that linear regressions of log chlorophyll on log TP explained about 90% of the variance in log chlorophyll (Dillon and Rigler, 1974; Schindler, 1978). (As both chlorophyll and TP in these plots spanned over 2 orders of magnitude, this does not necessarily mean that these regressions give precise chlorophyll estimates.) More recent analyses of data spanning a wider range of TP and chlorophyll have argued for a sigmoid relationship between log TP and log chlorophyll (Chow-Fraser et al, 1994).
Attempts to generalise on these early successes in temperate lakes by applying the models more broadly have met with mixed success. Both the prediction of TP from loads, and the prediction of chlorophyll from TP, have proven less straightforward in sub-tropical and tropical systems (Kaiser et al, 1994). The early results were obtained using annual average (or summer average) results from lakes with a very pronounced seasonal cycle in load, flushing and production. Australian lakes have highly intermittent loads, and much higher suspended sediment loads than Canadian lakes. It has also been suggested that nutrients other than phosphorus may be limiting at times (Harris, 1996), and statistical approaches to deal with this have been suggested (Kaiser et al, 1994).
There are a number of complications involved in applying the Vollenweider approach to estuaries (Harris, 1996). Estuaries are subject to flushing both through freshwater runoff and exchange with the ocean, and flushing rates cannot be simply calculated by dividing river flow by volume. (However, as discussed in Chapter 5, salt balance does allow effective flushing rates to be estimated simply.) Many estuaries have strong horizontal and vertical gradients, and treating these estuaries as simple well-mixed boxes may be quite inappropriate.
While limnologists have generally assumed that phosphorus is limiting in lakes, nitrogen is thought to be limiting in most marine systems. However, the situation in estuaries has been subject to considerable debate, and it is generally agreed that nitrogen, phosphorus and silicate can all be limiting at times in estuaries (Richardson and Jorgensen, 1996). (As noted above, this may also be true in freshwater systems see Harris, 1996.)
While the general mass balance principles underlying the Vollenweider models still apply in estuaries, it is not at all clear that the internal sink can be modelled in the same way. The principal sink for P in lakes may be adsorption to inorganic sediments, but marine sediments are known to be less effective at binding phosphate (Jorgensen, 1996). Where nitrogen is limiting, the principal internal sink may be denitrification rather than burial (Seitzinger, 1987, 1988, Harris et al 1996; Jorgensen, 1996). In undertaking mass balance for estuaries, it must be remembered that there is two-way exchange at the marine boundary, and coastal seawater contains a quite large concentration of total N, typically 50 to 100 mg N m-3. Part of this represents a refractory background pool of oceanic DON. This marine contribution not only affects the mass balance of TN, but is likely to complicate any empirical relationship between TN and chlorophyll in the estuary. This is especially the case when the estuary is subject to large catchment loads of organic N which, depending on the state of the catchment, may be labile or refractory (Harris, 1996).
Monbet (1992) has assembled data on 40 estuaries, and found a convincing relationship between mean annual DIN and chlorophyll. However, this relationship is only apparent when the estuaries are divided into microtidal and macrotidal (< 2 m and > 2 m tidal amplitude respectively). His log-log plot suggests that chlorophyll a increases roughly in proportion to DIN, although the residual scatter is large, and spans a factor of ca 2 about the mean. The proportionality constant is approximately 1 mg Chl a (mM N)-1 for macrotidal estuaries, and 10 mg Chl a (mM N)-1 for microtidal estuaries. If we assume a C:Chla ratio of 40, and a Redfield C:N ratio, there should be ca 2 mg Chl a (mM phytoplankton N)-1. This implies that (on an annual average basis) the phytoplankton N pool is about half the DIN pool in macrotidal estuaries, and 5 times the DIN pool in microtidal estuaries.
According to Monbets analysis, DIN is on average strongly utilized under conditions of weak tidal mixing, and only weakly utilized under conditions of strong tidal mixing. This is most likely due to the effects of increased vertical mixing on light availability to phytoplankton, either through increasing the mixed layer depth, or through an increase in suspended sediment and turbidity. This effect highlights the importance of turbidity and light attenuation in controlling utilization of nutrient (Harris, 1996), and raises the potential importance of sediment resuspension in controlling sediment nutrient fluxes and burial in estuaries.
Monbets analysis refers only to the relationship between DIN and chlorophyll, but DIN itself is likely to be a highly dynamic variable, not necessarily easily predicted from loads. In general, we would expect the proportion of TN present as DIN and phytoplankton N to increase, and the proportion present as refractory PON or DON to decrease, as systems become more eutrophic. In oligotrophic systems, the N load is dominated by inputs of refractory DON or PON from undisturbed catchments, and refractory DON from coastal waters. Loads from disturbed or agricultural catchments will contain increased amounts of DIN and labile organic N. Point source loads are generally dominated by DIN or labile organic N. In highly eutrophic systems, most of the TN load may consist of DIN, and a substantial fraction of this may remain unutilized due to light limitation.
In the course of this study, we have assembled 39 sets of observations of chlorophyll and nutrients in Australian estuaries and coastal embayments. DIN as a proportion of TN increases with increasing TN up to a maximum of 70% (Fig. 2.1), although the scatter also increases substantially at high TN. Phytoplankton N is less than 30% of total N, and as a percentage also appears to increase with TN, although again the scatter increases substantially at high TN (Fig 2.1). (Phytoplankton N is calculated assuming 2 mg Chl a (mM N)-1) . Because the size and composition of N loads are not known for many of these estuaries, it is not possible to tell whether the large scatter in these ratios is driven by variability in composition of loads, or variation in nutrient cycling and phytoplankton dynamics between estuaries.

|
| Fig. 2.1. DIN and Phytoplankton N as a fraction of Total N, plotted vs Total N, for observations drawn from a wide range of Australian estuaries.
(original size image) |
Biogeochemical models describe nutrient cycling and system responses in terms of pools and fluxes of nutrient. The state of the system at any given time is described by a set of state variables specifying the amount or concentration of nutrient contained in a series of functional components in a set of spatial cells. The time rate of change of these state variables is specified in terms of the physical transport in and out of spatial cells, and the local sources and sinks associated with biological and chemical reactions. We focus on local reactions here, and deal with physical transport in Chapter 5.
In this chapter, and in the rest of this report, we deal primarily with N-based models of estuarine eutrophication, consistent with the view that marine systems are generally N-limited. We do address other limiting nutrients below, and in Chapter 6.
The basic step in model definition is the selection of state variables or functional components. There is a widely accepted core set of components for marine biogeochemical models, namely DIN, Phytoplankton, Zooplankton and Detritus. These form the basis of so-called NPZ or NPZD models (Fennel, 1995; Murray and Parslow, 1997; Parslow, 1997). As we discuss below, either zooplankton or detritus may be omitted depending on the application. More complex biogeochemical models (eg Murray and Parslow, 1997, Radford, 1993, Evans and Garcon, 1997) represent elaborations of this core description. We discuss the reasons for these elaborations, and the implications of omitting them, at the end of this chapter.
To avoid confusion with the use of P for phosphorous, etc, we use DIN, PHY, ZOO and DET to represent DIN, phytoplankton, zooplankton and detritus pools here. In the following subsection, we describe standard formulations of the key biogeochemical / ecological processes which control exchanges among these pools.
Phytoplankton growth is obviously a critical step in the nitrogen cycle, affecting both the fate of DIN loads, and the phytoplankton biomass response. It is also arguably the best understood process in eutrophication, supported by a long history of laboratory and field studies of phytoplankton physiology and ecology (eg Harris, 1986, Falkowski and Woodhead, 1992). The phytoplankton specific growth rate m (d-1) is conventionally modelled as a maximum growth rate m max, reduced by dimensionless multiplicative factors for light and nutrient limitation:
| m = m max.hN.hI. | 3.1 |
Both hN and hI are typically formulated as saturating relationships eg the Monod relationship
| hN = DIN / (KN + DIN) | 3.2 |
where KN is the half-saturation constant for N-limited growth, and
| hI = 1. exp(-I/IK) | 3.3 |
where IK is the light saturation intensity (Platt and Jassby, 1976). More complex physiological models of nutrient uptake and growth (eg Droop, 1983; Tett et al, 1986) and alternative models of light limitation (Steele 1962, Platt and Jassby, 1976 ) are also used.
The light intensity experienced by phytoplankton depends not only on the surface light intensity, I0, but on the depth-distribution of phytoplankton, and light attenuation with depth. Light intensity at depth z is given by:
| I = I0.exp(-K.z) | 3.4 |
where K is the diffuse attenuation coefficient (m-1). (Where K varies with depth, K.z should be replaced by the depth integral of K from the surface to depth z.) In a well-mixed water column of depth H, the average light intensity <I> experienced by phytoplankton is given by:
| <I> = I0.(1 exp(-K.H))/(K.H) | 3.5 |
The attenuation coefficient K is a result of absorption and scattering by the water and optically active constituents such as inorganic sediment, detritus, coloured dissolved organic matter (CDOM) and phytoplankton chlorophyll. Their combined contributions can be approximated by a sum:
| K = K0 + k*CHL.CHL + k*DET.DET + k*DON.DON + | 3.6 |
where K0 is the background attenuation, and the k*X represent specific attenuation coefficients for constituents X. It is important to account for the effect of phytoplankton and other model components on light attenuation, and therefore on phytoplankton growth, because this represents a critical feedback (self-shading) at high phytoplankton biomass, under eutrophic conditions (see Chapter 4).
Phytoplankton biomass is lost as a result of grazing or other "natural" mortality, or through sinking and horizontal exchange. Phytoplankton biomass is determined by a balance between local growth and loss rates, so the prescription of loss rates is critical. There is much more uncertainty associated with the formulation of loss rates than growth rates.
In oligotrophic and mesotrophic conditions, loss rates are dominated by grazing. The NPZ models and their derivatives explicitly include zooplankton or other filter-feeders as dynamical state variables. These models then prescribe the phytoplankton consumption per unit zooplankton G as a function of phytoplankton biomass PHY (the so-called functional response). Commonly used formulations include a simple saturating response eg
| G = Gmax.PHY / (KP + PHY) | 3.7 |
where Gmax is the maximum consumption rate, and KP the half-saturation constant, and a response with reduced or zero clearance rates at low phytoplankton biomass eg
| G = Gmax.(PHY PHY0) / (KP + PHY PHY0) | 3.8 |
where PHY0 is a threshold below which grazing is zero. These are Holling Type II and TYPE III functional responses respectively (Holling, 1966).
An alternative approach is to omit the zooplankton state variable, and represent grazing losses along with other phytoplankton losses implicitly, as a specific phytoplankton mortality rate mP. This mortality rate is often treated as a constant, but may vary with phytoplankton biomass PHY (see below).
Where zooplankton are included explicitly, the phytoplankton consumption G is converted into a zooplankton growth rate by multiplying by a conversion efficiency EZ (the gross growth efficiency). The growth efficiency allows for losses associated with messy feeding, assimilation, and respiration and excretion. Some models represent respiration separately as an explicit loss process.
As well as physiological losses, zooplankton biomass is also lost to predation and "natural mortality". Very few models choose to represent carnivores explicitly, and predation is represented implicitly as a specific mortality rate. This truncation of the trophic chain is known as "trophic closure", and represents a significant unresolved issue for biogeochemical models (Totterdell et al, 1993).
Many NPZ models represent predation by a constant specific zooplankton mortality rate. Others use a specific mortality rate proportional to zooplankton biomass (total losses are then proportional to biomass squared and this is often referred to as quadratic mortality). Steele (1976), Steele and Henderson (1992) and Murray and Parslow (1997) have shown that the specification of zooplankton mortality rate has a profound effect on the stability and qualitative behaviour of NPZ models, and have argued that the quadratic formulation gives more realistic behaviour.
For a given functional response, G(PHY), and quadratic zooplankton mortality rate mQ.ZOO, the rate of change of zooplankton is given by:
| d ZOO / dt = EZ.G(PHY).ZOO mQ.ZOO2 | 3.9 |
The steady-state solution is
| ZOO = EZ.G(PHY)/mQ | 3.10 |
and the steady-state specific mortality rate exerted by zooplankton grazing on phytoplankton is then given by
| mP(PHY) = (EZ/mQ).G(PHY)2/PHY | 3.11 |
For example, if G(PHY) = Gmax.PHY/(KP + PHY), then
| mP(PHY) = (EZ/mQ).Gmax2.PHY/(KP + PHY)2 | 3.12 |
The increase in zooplankton biomass with increasing phytoplankton biomass is referred to as the numerical response. The expression given for mP(PHY) incorporates both the zooplankton functional and numerical response. We can use this expression to provide a more realistic formulation for mP in models where zooplankton are not represented explicitly. When used in a dynamical model, it is only an approximation, as it does not allow for the lags involved in the zooplankton numerical response to changes in phytoplankton abundance. These approximations are an unavoidable consequence of truncating the trophic chain at phytoplankton. Interestingly, in this formulation, m(PHY) increases linearly with PHY at low phytoplankton biomass (cf quadratic mortality for zooplankton), but declines at large PHY, as zooplankton numerical and functional responses saturate. This has important consequences for the qualitative behaviour of NPD models (see Chapter 4).
In NPZD or NPD models, phytoplankton and/or zooplankton losses are assumed to result both in direct production of DIN through zooplankton excretion, and in production of non-living organic N (detritus). The partitioning of phytoplankton losses between DIN and detritus may be fixed, or allowed to vary as a function of phytoplankton and zooplankton biomass. In general, the larger the fraction allocated directly to DIN, the higher the efficiency of nitrogen recycling in the water column.
In the water column, the detrital organic N is broken down over a range of time scales, both through bacterial attack and through ingestion by zooplankton, to release DIN. In simple NPZD or NPD models, this remineralization is represented by a constant specific breakdown rate, rDET. In more complex models, bacteria may be represented explicitly (eg Fasham et al, 1990). In NPD models, it can be argued that the "detritus" pool represents all non-photosynthetic organic matter, including living zooplankton and higher trophic levels. However, it is still treated as a single pool with a fixed breakdown rate.
The models described to this point have been used to address both open ocean biogeochemical cycles and coastal eutrophication. The key distinguishing feature of shallow coastal systems is the close coupling between water column and sediment, and the importance of sediment biogeochemistry. The coupling between water column and sediment occurs via settling and resuspension of particulate matter, especially detritus, and by diffusion and bio-irrigation of dissolved constituents, including DIN.
In the context of simple NP(Z)D models, the sediments are primarily a site for sedimentation and breakdown of detritus. Again, detrital breakdown occurs through a combination of bacterial attack and consumption by suspension and deposit feeders. Supply of oxygen is a major constraint on biogeochemical processes in the sediment, and there are a complex set of bacterially-mediated reactions controlled by oxygen concentration. Nitrification (conversion of ammonium to nitrate in oxic sediments) and denitrification (conversion of nitrate to N2 gas) are of particular importance for the nitrogen cycle, because nitrogen gas is inert, and denitrification represents a loss of TN from the combined water column-sediment system.
Quite complex models of sediment biogeochemistry have been developed (Blackburn and Blackburn, 1993; Boudreaux, 1997). These require fine depth and time resolution, because of the fine-scale gradients and rapid oxygen kinetics in the sediment, and are not suitable for incorporation in general eutrophication models. A key qualitative prediction from these models is that the denitrification efficiency (ie proportion of DIN produced through remineralization which is lost to denitrification) decreases as sediment respiration rates become large, and ultimately drops to zero as surface sediments become anoxic. This trend was confirmed in sediment flux studies in Port Phillip Bay (Harris et al, 1996), and Murray and Parslow (1997) used a simple empirical formula based on Port Phillip Bay data to relate denitrification efficiency EDEN to sediment respiration rate RSED:
| EDEN = EDENmax . (1 RSED/R0) | 3.13 |
where EDENmax is the maximum observed denitrification efficiency, and R0 is the respiration rate at which EDEN falls to zero.
Simple NP(Z)D models capture, at least in a crude sense, the major processes controlling the fate of nitrogen loads into coastal waters. Specifically, they represent nutrient uptake and growth by phytoplankton, the loss terms controlling phytoplankton biomass, the conversion and temporary accumulation of organic N as detritus, and the direct and indirect regeneration of DIN. With a simple sediment component added, they can also represent water column-sediment coupling, and the important internal sink of denitrification.
Simple models of this type have been used to represent nitrogen cycling and eutrophication in a number of applications (eg Fennel, 1995). However, other studies have adopted more complicated models (Radford, 1993; Murray and Parslow,1997). Here we review briefly the rationale for adopting more complex models, and the limitations involved in using simple models.
The simple NPZD models represent the nitrogen cycle, and the living and non-living organic components are normally represented as equivalent N concentrations (mg N m-3). One can convert these to carbon equivalents (or chlorophyll equivalents for phytoplankton) if one is prepared to assume a fixed stoichiometry. We noted earlier that phosphorus and silicate may at times be limiting or co-limiting in estuaries. The simple NPZD model can serve as a P-limited model, with minor adjustments to parameters to reflect the different stoichiometry. Denitrification of course has no equivalent in a P-based model, which should instead represent the adsorption of phosphate to inorganic material, and its dependence on oxic state and ionic strength.
In some estuaries, phosphorus is limiting in upstream low salinity waters and nitrogen in downstream marine waters. One can allow for both P and N limitation by explicitly representing the P and N content of all components separately, or by assuming fixed stoichiometry for the organic components, and duplicating only the dissolved inorganic pools. Silicate is normally a co-limiting nutrient, as it limits growth of siliceous phytoplankton (principally diatoms), but not others. Its principal effect may be to control phytoplankton composition, although there is evidence that it can also affect phytoplankton bloom magnitude (Murray and Parslow, 1997).
Some nitrogen-based models explicitly distinguish ammonium and nitrate. Phytoplankton take up ammonium in preference to nitrate, and may respond more quickly to ammonium enrichment. In oceanic systems, nitrification is thought to occur primarily below the euphotic zone, and so ammonium uptake is equated to regenerated production. It is important to distinguish ammonium and nitrate in explicit process models of sediment biogeochemistry, and they can serve as a useful diagnostic even where simple empirical sediment models are used (Murray and Parslow, 1997). Finally, in some estuarine systems where nitrate is present at very high concentrations in the water column, the flux of nitrate which diffuses into the sediment and is denitrified there is significant (Nielsen et al, 1994).
Some models represent more than one functional component at each trophic level. Plankton ecologists commonly separate both phytoplankton and zooplankton into size groups (eg pico-, nano- and micro- phytoplankton, and nano-, micro- and meso- zooplankton). These are useful both descriptively and as functional components. Small phytoplankton (pico and nano) are typically grazed by small zooplankton (nano and micro), which have rapid maximum growth rates, approaching or exceeding those of phytoplankton. It has been suggested that this rapid numerical response allows small zooplankton to control the biomass of small phytoplankton, and field observations show that small phytoplankton are typically present at relatively low background concentrations which respond only weakly to transient nutrient injections (Beardall et al, 1997).
Large phytoplankton, especially diatoms and dinoflagellates, are typically grazed by crustaceans with slow numerical responses, and appear able to escape grazing control and form blooms in the presence of excess nutrients. It could be argued models of eutrophication should concentrate on representing the dynamics of bloom phytoplankton. However, explicitly including both small and large phytoplankton may allow models to represent the transition from oligotrophic or mesotrophic to eutrophic conditions.
Different nutrient requirements provide another reason for distinguishing phytoplankton functional groups. Diatoms require silicate, and diatom bloom magnitude may be constrained by silicate limitation. In fresh and brackish waters, N-fixing cyanobacteria are favoured by excess phosphate and low DIN. It is still puzzling (and fortunate) that N-fixing cyanobacterial blooms appear to be rare in temperate and subtropical coastal waters (but see Chapter 7).
Some models have included higher trophic levels, extending to carnivorous zooplankton and fish (eg Radford, 1993). These models have generally been more concerned with the ecology of higher trophic levels than with their top-down effects on eutrophication. At least in marine systems, integration of biogeochemical models of lower trophic levels with ecological or population models of higher trophic levels is still poorly developed.
The NPZD models represent only one pool of non-living organic matter, which is assigned a characteristic remineralization time scale. In practice, the non-living organic matter pool consists of both dissolved and particulate matter, and includes both labile and refractory compounds. The sources and fates of these components may also differ widely. Particulate detritus is subject to sedimentation, is more likely to be recycled or buried in the sediment, and is therefore strongly linked to internal sinks. Dissolved organic nitrogen is more likely to be exported from the estuary, especially if it is refractory.
Catchment runoff can act as a significant source of both dissolved and particulate organic N. This material is more likely to be refractory if the catchment is relatively undisturbed. As noted above, seawater at the estuary mouth will generally contain quite high concentrations of DON, most of which may be refractory.
Refractory DON and PON are likely to dominate the water column TN pool in most estuaries, and therefore to dominate the export of nitrogen from the estuary. It follows that, if models are to reproduce TN observations and N budgets, they need to explicitly represent refractory material. On the other hand, the labile detrital pools control the sedimentation of organic matter from phytoplankton production, and consequently sediment respiration and denitrification sinks. Thus, there are strong arguments to divide the detrital pool into at least two functional components, even in simplified eutrophication models.
Our understanding of the processes controlling production and consumption of refractory PON and DON (on time scales of months to years) is poor, and this is an area deserving further research. In fact, monitoring programs usually measure total organic N (or TKN), but do not discriminate DON from PON (this is relatively straightforward) or refractory and labile ON (this is not). This makes it very difficult to allocate loads or boundary concentrations of organic N to model functional components.
The NPZD models represent only planktonic primary producers. Phytoplankton blooms are often the primary concern in eutrophication, and are the principal focus of this study in particular. However, benthic plants such as seagrass, macroalgae and microphytobenthos can be major or dominant primary producers in shallow coastal systems. It is possible to represent these explicitly in eutrophication models (Murray and Parslow, 1997). The formulation for nutrient uptake and growth by benthic plants is basically similar to that for phytoplankton, except that benthic plants respond to bottom light levels (and are therefore much more sensitive to changes in light attenuation), and seagrass and microphytobenthos have access to nutrients in sediment pore waters.
Benthic filter feeders can make an important and even dominant contribution to phytoplankton grazing in shallow coastal systems (eg Clapham, 1996). They can also serve to increase the effective sedimentation rate of organic matter. It is again relatively straightforward to represent these explicitly in models, using similar grazing, growth and mortality formulations to those used for zooplankton.
A truly comprehensive and versatile model of coastal biogeochemistry and eutrophication might be expected to incorporate all the processes described above. Examples of models with this kind of scope include the Port Phillip Bay Integrated Model (Murray and Parslow, 1997) and the North Sea ERSEM model (Radford, 1993). The N cycle represented in the Port Phillip Bay model is shown schematically in Fig. 3.1. The ERSEM model is still more complex. Model complexity of this order offers realism and versatility, but at the expense of increased requirements for field surveys and process studies for model calibration. The Port Phillip Bay model contains 18 state variables and 70 parameters. Model calibration and analysis required extensive effort and was only possible because an unusually comprehensive program of observations and process experiments was conducted as part of the Port Phillip Bay Environmental Study (Murray and Parslow, 1997).
The NPD model formulation involves significant simplifications and approximations. These will result in acceptable errors in some circumstances, while the model may not be applicable at all in others. However, where eutrophication problems involving major algal blooms in urban estuaries result from large point source or diffuse loads of available nitrogen, the NPD models incorporate the core processes needed to address them. Because of their simple structure and small number of variables and parameters, these models can be implemented and calibrated relatively quickly using the results of routine monitoring (see Chapter 6).
 |
| Fig. 3.1. Nitrogen cycling in the Port Phillip Bay Integrated Model. |
In Chapter 3, we argued that a simple NPD biogeochemical model should be able to capture many of the key processes controlling nitrogen cycling and phytoplankton biomass in estuaries. This chapter analyses the steady-state behaviour of a model of this kind. The chapter includes some moderately detailed equations and algebra, which we have enclosed in boxes. Readers who don't wish to follow the analysis in detail may wish to skip over the boxes. Those who are interested only in the principal conclusions may jump to the concluding section of this Chapter.
The model is implemented within the simplest possible physical context, representing the estuary as a single well-mixed compartment, with a prescribed flushing rate r (d-1). Sediment pools, and sediment water column exchanges, are represented implicitly by assuming that a fixed proportion s of the total pool of each particulate component is suspended in the water column, with the remainder in the sediment. This is a reasonable approximation, at least in shallow waters where exchange between water column and sediment is likely to be dominated by physical processes of sinking and resuspension. The suspended fraction s is subject to horizontal transport (ie flushing), while the sedimented fraction (1-s) is subject to benthic remineralization and denitrification.
The model includes 4 state variables: phytoplankton biomass (PHY), DIN, labile organic detritus (DET) and refractory organic detritus (REF). Depending on the assigned suspended fraction, DET and REF can be treated as particulate or dissolved. All variables are defined in nitrogen equivalent concentrations as mg N m-3 and all fluxes as mg N m-3 d-1.
The dynamical equations defining the model are:
| dDIN/dt = LDIN - m.PHY + (1-fDET).m.PHY + (1-EDEN).RSED + RW - r.(DIN - DINO) | 4.1 |
| dPHY/dt = m.PHY m.PHY - r.(PHY-PHYO) | 4.2 |
| dDET/dt = LDET + fDET.m.PHY - rDET.DET - r .(sDET.DET - DETO) | 4.3 |
| dREF/dt = LREF + fREF.rDET.DET - rREF.REF - r.(sREF.REF - REFO) | 4.4 |
In each equation, LX represents the load, and XO the ocean concentration, of constituent X. In Eq 4.1 and 4.2, m is the phytoplankton growth rate, m the phytoplankton loss rate, fDET the proportion of phytoplankton loss assigned to DET, RSED is the sediment respiration rate, EDEN the denitrification efficiency, and RW is the water column respiration rate. In Eq 3 and 4, rDET and rREF are the breakdown rates of labile and refractory detritus, and fREF is the proportion of labile detritus converted to refractory detritus.
As discussed in Chapter 3, the phytoplankton growth rate is given by:
| m = mmax.hN.hI | 4.5 |
where hN = DIN / (KN + DIN).
The light limitation term hI is based on a depth integrated version of Steele's (1962) equation:
| hI = (exp(1. 2.exp(-K.H)) exp(-1)) / (K.H) | 4.6 |
where H is estuary depth. The light attenuation coefficient K is given by:
| K = KO + k*PHY.PHY + k*DET.DET + k*REF.REF | 4.7 |
Following the discussion in Chapter 3, the phytoplankton mortality rate is given by
| m(PHY) = m0 + 4.m1.PHY/(KP + PHY)2 | 4.8 |
and has a maximum value m0+m1 at PHY = KP. The sediment respiration rate is given by:
| RSED = rDET.(1-sDET).DET . (1-fREF) + rREF.(1-sREF).REF | 4.9 |
and the water column respiration rate is given by
| RW = rDET.sDET.DET . (1-fREF) + rREF.sREF.REF | 4.10 |
The denitrification efficiency EDEN is given by
| EDEN = EDENmax . (1 RSED / R0) | 4.11 |
If Eq 4.1 to 4.4 are summed, the internal transformations of N cancel out, yielding
| d TN / dt = LTN - r .(TNW TNO) EDEN.RSED | 4.12 |
where TN is total nitrogen in the system (TN = DIN+PHY+DET+REF), and TNW is total nitrogen in the water column (TNW = DIN + PHY + s
DET.DET + s
REF.REF). At steady-state,
| LTN = r .(TNW TNO) + EDEN.RSED | 4.13 |
that is, Load = Net Export + Internal Sink. We can also rewrite Eq 4.13 as
| TNW = TNO + (LTN EDEN.RSED) / r | 4.14 |
Equation 4.14 is the equivalent of Vollenweider's equation for N-limited estuaries. As for lakes, the flushing rate r plays a dominant role in determining the concentration of TN in the water column. In the absence of any internal sink, the entire N load is exported to the ocean, and TN is increased above the ocean background by TN* = LTN/r , the concentration needed to flush the load out of the estuary. TN is reduced below TN* according to the proportion of the total N load lost to the internal sink rather than exported from the estuary.
The steady-state equations are just:
| 0 = LDIN - m .PHY + (1-fDET).m.PHY + (1-EDEN).RSED + RW - r .(DIN - DINO) | 4.15 |
| 0 = m .PHY m.PHY - r .(PHY-PHYO) | 4.16 |
| 0 = LDET + fDET.m.PHY - rDET.DET - r .(s DET.DET - DETO) | 4.17 |
| 0 = LREF + fREF.rDET.DET - rREF.REF - r .(s REF.REF - REFO) | 4.18 |
It is possible to solve Eq 4.16 to 4.18 explicitly for DIN, DET and REF in terms of PHY. These solutions determine the relative composition of the TNW pool as a function of TNW.
First, Eq 4.17 can be rearranged to give
| DET = (LDET + fDET.m.PHY + r .DETO )/(rDET + r .s DET). | 4.19 |
The sum rDET + r
.s
DET is the combined physical and biological turnover rate of labile detritus in the system, while LDET and fDET.m.PHY represent the external and internal loads of labile detritus. The concentration of DET resulting from internal production is
| DETI = fDET.m.PHY / (rDET + r .s DET) | 4.20 |
Thus, DETI/PHY increases as mortality rate m increases, and decreases as remineralisation (rDET) and flushing rate (r ) increase. DET/PHY increases as s DET decreases (that is, more detritus accumulates in bottom sediments if the suspended fraction is low), but the concentration of detritus suspended in the water column, s DET.DET, increases as s DET increases.
Next, Eq 4.18 can be rearranged to give
| REF = (LREF + r .REFO + fREF.rDET.DET) / (rREF + r .s REF) | 4.21 |
Again, rREF + r
.s
REF is the combined turnover rate of refractory detritus. The refractory detritus produced internally, REFI, is present in fixed ratio to the labile detritus DET:
| REFI = (fREF.rDET / (rREF + r .s REF)) . DET. | 4.22 |
The concentration of refractory detritus in the water column is given by s REF.REF, and increases with s REF.
Last, Eq 4.19 gives
| m .PHY = (m + r ).PHY + r .PHYO | 4.23 |
If we assume PHYO is small compared with PHY (likely to be true for eutrophic estuaries), then
| m » m + r | 4.24 |
Recall that m
= m
max.hN.hI, where hN = DIN/(KN+DIN), and hI depends on light limitation and light attenuation, and therefore on PHY, DET and REF through Eq 4.6 and 4.7. The mortality rate m is also a function of PHY (Eq 7). Substituting in Eq 4.24 gives:
| hN » (m(PHY) + r ) / (m max.hI) = hN*(PHY), | 4.25 |
where hN*(PHY) depends explicitly on PHY through m(PHY), and implicitly on PHY, DET and REF via hI and K.
We can then solve Eq 4.25 explicitly for DIN:
| DIN = KN . hN* / (1 hN*) | 4.26 |
Note that DIN is scaled by the half-saturation constant KN.
hN* is just the ratio of the phytoplankton loss rate to the light-limited nutrient-saturated phytoplankton growth rate, m
I = m
max.hI. At steady-state, the DIN concentration must be such as to reduce phytoplankton growth rates by a factor hN*. At low values of PHY, the model constituents make an insignificant contribution to light attenuation, so K »
K0, hI is constant, and hN* is proportional to m(PHY) (Fig. 4.1). However, as PHY increases, phytoplankton and detritus make an increasing contribution to light attenuation, K increases, hI decreases, and hN* increases steeply. Eventually, at very high values of PHY, hN* exceeds 1. But hN = DIN/(KN+DIN) cannot exceed 1. The phytoplankton concentration PHYmax where hN* = 1 represents a maximum upper limit to phytoplankton biomass due to self-shading.

|
| Fig. 4.1. Change in N-limitation factor hN* with phytoplankton biomass PHY |
| (original size image) |
For each value of PHY (and for given boundary conditions and loads LDET, LREF), we can use Eq 4.19, 4.21 and 4.26 to compute the corresponding values of DIN, DET and REF. We can then substitute these in Eq 4.15 to obtain an explicit relationship between PHY and LDIN:
| LDIN = L*(PHY) | 4.27 |
For a given DIN load LDIN, Eq 4.27 can be inverted to find the corresponding value of PHY, and hence the corresponding values of DIN, DET and REF.
We consider first a simple example in which there is no internal sink (ie denitrification is switched off), and the nitrogen load consists only of DIN. We also assume the ocean concentrations are negligible. Then the water column TN pool is just given by TNW = LDIN/r (Eq 4.14), and all the organic matter present must be produced internally through phytoplankton production and mortality.
We illustrate the model behaviour with two examples, one for a low flushing rate (r = 0.01 d-1), and one with a high flushing rate (r = 0.1 d-1). The parameter values for these and later examples are given in Table 4.1.
For a low flushing rate of 0.01 d-1 (Fig 4.2), TNW increases from 100 to 10000 mg N m-3 as load increases from 1 to 100 mg N m-3 d-1. PHY increases more or less in proportion to load up to about 300 mg N m-3 (40 mg Chl a m-3), but then asymptotes to a PHYmax value of 420 mg N m-3 (60 mg Chl a m-3) due to self-shading (cf Fig. 4.1). PHY constitutes about 30 to 40% of the TNW pool for loads below 10 mg N m-3 d-1, but declines in importance at higher loads. DIN is very low in relative and absolute terms at low loads, but dominates the TNW pool at very high loads, as phytoplankton uptake of DIN becomes light-limited due to self-shading. The detrital pools decline from 30% (refractory) and 20% (labile) of TNW at low loads to less than 20% for loads above 10 mg N m-3 d-1.
| Symbol | Description | Units | Value |
|---|---|---|---|
| mmax | Maximum phytoplankton growth rate | d-1 | 1.5 |
| KN | Half-saturation constant for phytoplankton growth on DIN | mg N m-3 | 10 |
| m0 | Background constant phytoplankton loss rate | d-1 | 0.1 |
| m1 | Maximum grazing loss rate | d-1 | 0.4 |
| KP | Phytoplankton biomass corresponding to maximum grazing loss rate | mg N m-3 | 20 |
| fDET | Fraction of grazing losses to labile detritus | 0.5 | |
| fREF | Fraction of labile detritus to refractory detritus | 0.2 | |
| rDET | Breakdown rate of labile detritus | d-1 | 0.1 |
| rREF | Breakdown rate of refractory detritus | d-1 | 0.01 |
| EDENmax | Maximum denitrification efficiency | 0-0.7 | |
| R0* | Sediment respiration rate at which EDEN = 0. | mg N m-2 d-1 | 250 |
| K0 | Background light attenuation | m-1 | 0.1-0.9 |
| k*PHY | Specific light attenuation for phytoplankton | m2 (mg N)-1 | 0.0035 |
| k*DET | Specific light attenuation for labile detritus. | m2 (mg N)-1 | 0.0035 |
| k*REF | Specific light attenuation for refractory organic N | m2 (mg N)-1 | 0.0009 |
| sDET | Suspended fraction of labile detritus | 0.3 | |
| sREF | Suspended fraction of refractory organic N | 0.3 | |
| H | Depth | m | 10 |
| r | Flushing rate | d-1 | 0.1-0.01 |
| Table 4.1. Parameter set used for steady-state examples. See text for details where a range of values is given. | |||
For a high flushing rate of 0.1 d-1 (Fig. 4.3), TNW increases from 10 to 1000 mg N m-3 as load increases from 1 to 100 mg N m-3. PHY is about 40% of TNW for loads less than 10 mg N m-3 d-1, but increases to almost 60% of TNW at a load of 30 mg N m-3 d-1, before saturating at a PHYmax value of 250 mg N m-3 (mg Chl a m-3). The detrital fraction of TNW peaks at about 25% (labile) and 15% (refractory) at a load of 10 mg N m-3 d-1. The labile pool is now larger than the refractory pool, because the high flushing rate does not allow high concentrations of refractory detritus to accumulate. The DIN concentration is increased substantially at low loads, in order to support the increased phytoplankton growth rate required to balance the flushing rate. Again, DIN dominates the TN pool at very high loads, as phytoplankton uptake becomes light-limited due to self-shading.

|
| Fig. 4.2. Change in concentrations of TNW and PHY vs load, and change in composition of TNW vs TNW concentration, for r = 0.01 d-1, K0 = 0.2 m-1, DEN = 0. |
| (original size image) |
Thus, for both low and high flushing rates, the model predicts an oligotrophic to mesotrophic regime (PHY < 40 mg N m-3, or about 6 mg Chl a m-3) where relative composition of TN is fairly constant, a transition region where biomass increases further and phytoplankton start to escape grazing control, but DIN remains low, and a highly eutrophic region where phytoplankton biomass is so high that self-shading reduces growth rates and DIN accumulates.

|
|
Fig. 4.3. Change in concentrations of TNW and PHY vs load, and change in composition of TNW vs TNW concentration, for r = 0.1 d-1, K0 = 0.2 m-1, DEN = 0. |
| (original size image) |
d) Effect of Background Light Attenuation K0.
PHYmax is the upper limit to phytoplankton biomass imposed by self-shading. PHYmax depends strongly and very non-linearly on the background light attenuation K0. For example, for the standard parameter values used here, PHYmax declines slowly as K0 increases from 0.1 to 0.7, then falls suddenly by more than an order of magnitude as K0 increases to 0.8 (Fig. 4.4).
The reason for this can be seen in Fig. 4.5, which plots hN* vs PHY for values of K0 from 0.1 to 0.9. Recall that PHYmax is determined by the condition hN* = 1. As K0 increases, hN* increases for all PHY. Because there is a local minimum in hN* at intermediate values of PHY, PHYmax drops suddenly as this minimum approaches 1.
With K0 = 0.9 m-1, PHY saturates at relatively low levels of about 7 mg N m-3 (1 mg Chl a m-3) at a low load of about 1 mg N m-3 d-1, and the TN pool is dominated by DIN at all loads (Fig. 4.6).

|
| Fig. 4.4. Variation in PHYmax with increasing background light attenuation K0. |
| (original size image) |

|
| Fig. 4.5. Effect of increasing K0 on hN*(PHY). Plotted curves from bottom to top correspond to K0 values of 0.1, 0.2, 0.4, 0.6, 0.7, 0.8 and 0.9 m-1. |
| (original size image) |

|
| Fig. 4.6. Change in concentrations of TNW and PHY vs load, and change in composition of TNW vs TNW concentration, for r = 0.01 d-1, K0 = 0.9 m-1, DEN = 0 |
| (original size image) |
The model suggests that light attenuation exerts a powerful and non-linear control on phytoplankton biomass in estuaries. For estuaries with low background attenuation, high nutrient loads will produce very high phytoplankton biomass. However, as background attenuation increases, the maximum achievable phytoplankton biomass will drop to low levels, and high DIN concentrations will accumulate. (The Brisbane River estuary represents a classic example of this second type.)
Note that the background attenuation K0 enters Eq 4.25 through Eq 4.6 as the product K.H, suggesting that it is really the product of K0 and depth H which controls PHYmax. Model solutions bear this out: increases in depth H or attenuation K0 are equally effective in reducing PHYmax (for the well-mixed water column considered here).
For each PHY, hN*(PHY) represents the ratio of the phytoplankton loss rate to the light saturated growth rate, and therefore the proportional reduction in growth due to nutrient limitation required for growth to balance losses. Values of PHY for which hN*(PHY) equals 1 are values where nutrient-saturated growth equals losses; ie where (at sufficiently high DIN loads) a steady-state with very high DIN concentrations is possible. Because the mortality function m(PHY) (Eq 4.8) has a maximum value at PHY = KP, and declines at large PHY, the function hN*(PHY) can have a minimum at intermediate values of PHY. Fig. 4.5 shows that this can result in a situation where hN*(PHY) equals 1 at three different values of PHY. Each corresponds to a possible system steady-state with very high DIN concentrations. The upper value is just the self-shaded condition already discussed, with PHY = PHYmax. The steady-state corresponding to the middle value is unstable, but the lower value PHY* corresponds to a stable state in which light-limitation is not important, and phytoplankton biomass is controlled at low levels by zooplankton grazing.
It is not clear whether grazing controlled steady-states of this kind really occur in estuaries subject to high nutrient loads. As discussed in Chapter 3 (and later in Chapter 7), while some phytoplankton functional groups may be controlled by grazers, opportunistic bloom species which can escape grazing control seem able to exploit most situations with ample light and elevated nutrient concentrations.
We now consider the same examples, but with denitrification switched on. For a low flushing rate, denitrification is effective for loads below about 5 mg N m-3 d-1, removing about 70 to 80 % of the input load (Fig. 4.7). This means that TNW is reduced by 70 to 80% below the levels predicted without denitrification. However, once the load exceeds about 7 mg N m-3 d-1, sediment respiration rates exceed the rate R0 at which denitrification drops to zero. TN then suddenly increases about 5-fold to the level required for export to balance loads. The relative composition of TN is not too different from that predicted without denitrification, so that phytoplankton biomass is also reduced 4 to 5 fold at loads less than 5 mg N m-3 d-1, and increases 5-fold when the critical load is exceeded, approaching the self-shaded limit PHYmax.
This dramatic non-linear response to increasing loads is a direct result of the postulated decrease in denitrification efficiency with increasing sediment respiration rate (Eq 11). It was one of the key findings of the Port Phillip Bay Environmental Study (Harris et al, 1996, Murray and Parslow, 1997). The significance of this effect depends on the relative importance of denitrification and export at intermediate loads. This effect is most important for estuaries or embayments with very long flushing times. (The flushing time for Port Phillip Bay is about 1 year, corresponding to r = 0.003 d-1.)
For a high flushing rate of 0.1 d-1, denitrification accounts for a maximum of only about 25% of the DIN load (Fig. 4.8). As a result, TN and PHY are reduced only slightly below the values obtained without denitrification. In this case, the predicted sediment respiration rates are not sufficient to switch denitrification off even at very high loads, and the model predicts a smooth transition from an N-limited state with moderate denitrification efficiency to a light-limited state with low denitrification efficiency and high DIN.

|
| Fig. 4.7. TNW, PHY vs load, TNW composition vs TNW, and denitrification flux as a fraction of total load vs load, for r = 0.01 d-1, K0 = 0.2, and EDENmax = 0.7. |
| (original size image) |

|
| Fig. 4.8. TNW, PHY vs load, TNW Composition vs TNW, and denitrification flux as a fraction of total load vs load, for r = 0.1 d-1, K0 = 0.2, and EDENmax = 0.7. |
| (original size image) |
These results suggest that denitrification reduces TN and phytoplankton biomass in the same proportion as it reduces N loads. The steady-state equations offer further insight into the factors controlling the fraction of the N load removed by denitrification at low loads, and the critical load for denitrification shutdown, where this occurs.
Recall that the denitrification flux is given by:
|
DEN = EDEN . RSED = EDEN . (rDET.(1-sDET).DET . (1-fREF) + rREF.(1-sREF).REF). |
4.28 |
The export flux is just:
| EXPORT = r . (PHY + DIN + sDET.DET + sREF.REF). | 4.29 |
Recall moreover that:
| DET = fDET.m.PHY / (rDET + r.sDET). | 4.30 |
The amount of primary production directed to detritus is directly controlled by fDET, the fraction of grazing losses assigned to detritus. Increases in fDET will increase sediment respiration relative to water column respiration, and therefore enhance denitrification.
The fraction of labile and refractory detritus suspended in the water column is given by s DET and s REF respectively. Increases in these suspended fractions decrease denitrification relative to export by both increasing the suspended detritus fraction subject to flushing, and increasing water column recycling relative to sediment recycling, where denitrification occurs.
The respiration rates rDET and rREF control the respiration rates of sedimented detritus. As respiration rates increase relative to flushing rates, more detritus is recycled internally and less is exported.
The denitrification efficiency is assumed to decrease as RSED increases, and
| DEN = EDENmax . RSED . (1 RSED / R0). | 4.31 |
DEN varies quadratically with RSED, and reaches a maximum of EDENmax.R0/4 at RSED = R0/2. Provided flushing rates are low, this maximum denitrification flux is a close approximation to the critical load. Note that R0 is strictly defined as a rate per unit area, but all model variables and fluxes are defined as rates per unit volume. Thus, R0 = R0*/H, where R0* is the underlying respiration rate per unit area (mg N m-2 d-1). For R0* = 250 (the value used in Port Phillip Bay, see Murray and Parslow, 1997), and a 14 m water column, the critical load is predicted to be 4.5.EDENmax, or about 2 to 3 mg N m-3 d-1. Note that the critical load is better specified as an areal load of about 30 mg N m-2 d-1, independent of depth.
This calculation of the critical load assumes that denitrification accounts for most of the external load. We have seen that, if flushing rates are high, denitrification accounts for a small fraction of the load, and there is no critical load corresponding to an abrupt transition in biomass. We have also seen that, in turbid estuaries, even at low flushing rates, phytoplankton biomass is restricted to low levels by light limitation, and most of the DIN load is exported unutilised. Under these circumstances, there is also no abrupt transition or critical load.
In estuaries where high levels of DIN accumulate, ammonium may be nitrified in the water column producing high nitrate concentrations. Nitrate can then diffuse into the sediment where it is denitrified. The model as formulated does not allow for this process. It is only important when water column DIN levels are already very high ie where phytoplankton uptake and growth are already saturated, so is not likely to critically affect predictions of phytoplankton biomass. High light attenuation may favour this process because reduced light intensities not only inhibit phytoplankton uptake of ammonium, but encourage nitrifying bacteria, which are thought to be photo-inhibited (Lipschultz et al, 1985; Ward, 1985).)
In the analysis so far, we have assumed that the catchment nitrogen load consists only of DIN. Where point source loads dominate, and effluent is secondary treated, loads will indeed be mostly DIN. However, as we have already noted, diffuse loads from catchment runoff contain appreciable amounts of organic nitrogen. In pristine catchments, most of this organic nitrogen may be refractory. As catchments are modified, an increasing proportion may be made up of labile detritus.
We have also ignored until now the concentrations of DIN, phytoplankton and detrital N in marine waters. Exchange at the mouths of estuaries effectively constitutes an additional load of nitrogen which is missing in lakes. While the marine concentrations of DIN and phytoplankton N may be quite low, concentrations of refractory organic N in marine waters are significant.
With DIN loads alone, the model predicts that phytoplankton N should form the largest single fraction of TN at low to intermediate loads, with a comparable contribution from the combined detrital pools (Fig. 4.2, 4.3). But observations show that detrital N dominates the TN pool at low loads, with phytoplankton N making up a minor component (Fig. 2.1). This is attributable to the contribution of detrital N loads from both catchment runoff and ocean.
We derived above Eq 4.19 and 4.22 for the steady-state concentrations of labile and refractory detritus:
DET = (LDET + r .DETO + fDET.m.PHY)/(rDET + r .s DET).
REF = (LREF + r .REFO + fREF.rDET.DET) / (rREF + r .s REF).
The steady-state concentrations of detritus are directly increased by L/(r + r .s ), and the fraction of the detritus load remineralized in the estuary (rather than exported) is given by r.L/(r + r .s ).
For estuaries with low flushing rates, of order 0.01 d-1, the remineralization rate of labile detritus is much larger than the flushing rate, and most of the labile detritus should be consumed within the estuary, contributing to phytoplankton production. The remineralization rate of refractory detritus may then be comparable to flushing rates, and a substantial fraction may be remineralized within the estuary. For the parameters in Table 4.1, the steady-state concentration of refractory detritus will be about 20 times that of labile detritus for the same load at very low flushing rates.
For estuaries with high flushing rates, of order 0.1 d-1, the labile remineralization rate and flushing rate will be comparable, while the refractory remineralization rate is much lower. Now most of the refractory detritus load and a substantial proportion of the labile detritus load will be exported. Because flushing dominates, the steady-state concentrations of labile and refractory detritus will be comparable for equal loads.
To illustrate these effects, we look at the effect of increasing DIN loads on estuaries with fixed background loads of labile and/or refractory detritus, under high or low flushing rates. The first two examples represent an estuary with low flushing rate (0.01 d-1), background levels of oceanic refractory organic N (REFO = 60 mg N m-3), and moderate loads of labile or refractory detritus (1 mg N m-3 d-1).
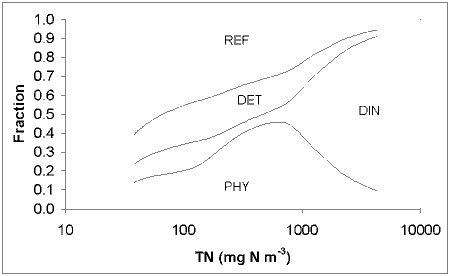
|
| Fig. 4.9. TNW composition vs TNW for varying DIN load from 1 to 100 mg N m-3 d-1, with an oceanic boundary concentration REFO = 60 mg N m-3, and a fixed load of labile detritus LDET of 1 mg N m-3 d-1 (r = 0.01 d-1). |
| (original size image) |
Due to the ocean source, refractory detritus becomes the dominant N pool in the estuary in both examples (Fig. 4.9, 4.10). With a labile load from the catchment, refractory detritus constitutes 60% of the TN pool at low DIN loads. With a refractory load from the catchment, refractory detritus reaches 80% of the TN pool at low DIN loads.

|
| Fig. 4.10. TNW composition vs TNW for varying DIN load from 1 to 100 mg N m-3 d-1, with an oceanic boundary concentration REFO = 60 mg N m-3, and a fixed load of refractory detritus REF of 1 mg N m-3 d-1 (r = 0.01 d-1). |
| (original size image) |

|
| Fig. 4.11. TNW composition vs TNW for varying DIN load from 1 to 100 mg N m-3 d-1, with an oceanic boundary concentration REFO = 60 mg N m-3, and a fixed load of labile detritus DET of 1 mg N m-3 d-1 (r = 0.1 d-1). |
| (original size image) |

|
| Fig. 4.12. TNW composition vs TNW for varying DIN load from 1 to 100 mg N m-3 d-1, with an oceanic boundary concentration REFO = 60 mg N m-3, and a fixed load of refractory detritus REF of 1 mg N m-3 d-1 (r = 0.1 d-1). |
| (original size image) |
The second two examples use the same marine boundary concentrations and loads with a high flushing rate (0.1 d-1). Now, the contribution of refractory detritus increases to 80% TN with a labile detritus load, and 90% TN with a refractory detritus load (Fig. 4.11, 4.12). By comparison, the labile detrital pool remains low at low DIN loads. Even with a labile detritus load of 1 mg N m-3 d-1, the labile detrital pool is comparable to the phytoplankton N pool.
These examples illustrate the importance of the marine background organic N (DON) in determining TN concentrations and composition at low loads, under oligotrophic conditions. Observations show a shift in TN composition with increasing enrichment from predominantly detrital N to increasing DIN (Fig. 2.1). This can be explained by a shift in load composition from refractory organic N (of marine and catchment origin) to labile detritus and DIN, combined with a reduction in utilization of DIN at high loads due to increased turbidity and phytoplankton self-shading.
Simple load-response models have proven less effective in estuaries, which show considerable variability in their response to nutrient loads. The simplified process models analysed here provide insight into that variability.
As in lakes, flushing rates play a dominant role in controlling estuarine response to nutrient loads. To a first approximation, for a given load, concentrations of total nitrogen in the estuary are inversely proportional to flushing rate. However, flushing is a more complicated process in estuaries than in lakes, involving not only throughflow of freshwater, but tidal or estuarine exchange with seawater at the mouth. This not only means that flushing rates can vary widely, depending on the estuarine morphology and tidal regime, but that the contributions of nitrogen at the marine boundary must be taken into account. Even oligotrophic marine waters have moderate concentrations of refractory DON, and these can make a significant contribution to estuarine TN concentrations when catchment loads are low. At temperate latitudes, marine waters can also be a significant source of DIN in winter (see Section 6.1).
Vollenweider's steady-state mass-balance still applies in estuaries, once catchment and marine sources are taken into account. The total nitrogen concentration must be sufficient for export to balance loads after internal sinks are taken into account. Denitrification can be a major internal nitrogen sink in estuaries, and can account for most of the nitrogen load when flushing rates are very low, as in Port Phillip Bay (Murray and Parslow, 1997). Under these conditions, denitrification can reduce TN, and phytoplankton biomass, by almost an order of magnitude below the levels expected in the absence of denitrification, shifting the system from eutrophic to mesotrophic.
As nutrient loads increase, phytoplankton production and sediment respiration rates also increase, leading to greater oxygen stress in bottom sediments. Denitrification efficiency declines as sediments become anoxic. This feedback creates an instability in simple 1-box models. As nutrient loads exceed a critical threshold level, denitrification shuts down, and phytoplankton biomass and DIN jump to eutrophic levels. This threshold load is primarily determined on an areal basis by the sediment biogeochemistry, and was found to be of order 30 mg N m-2 d-1 in Port Phillip Bay.
When flushing rates are high, denitrification accounts for a minority of the nitrogen load, and the instability disappears. The significance of denitrification relative to export depends not only on the flushing rate, but also on parameters controlling the proportion of phytoplankton production (or external detrital loads) which is remineralized in the sediment, versus the proportions remineralized in the water column or exported. These parameters include eco-physiological parameters such as fDET, the proportion of phytoplankton mortality converted to detritus, and physical parameters, especially the sinking and resuspension rates which control the proportion of organic detritus which remains in suspension. This suspended fraction can vary widely in estuaries, because of differences in depth and the importance of tidal currents and wind-driven currents and waves.
Phytoplankton biomass and detritus concentrations increase as loads of available N increase, but this increases light attenuation. Under eutrophic conditions, there is an upper limit to phytoplankton biomass and production imposed by self-shading. Once this biomass is reached, further increases in loads of available N are not utilized and accumulate as high concentrations of DIN. The self-shaded limit depends strongly and non-linearly on the estuary depth and background turbidity. Estuaries with naturally high levels of suspended sediments or humics can be light-limited at quite low phytoplankton biomass. These estuaries (eg Brisbane River) can accumulate very high concentrations of DIN without significant algal blooms. Monbet (1992) found that plots of chlorophyll vs TN separated estuaries into microtidal and macrotidal. This almost certainly reflects differences in background turbidity and available light, as well as differences in the suspended fractions of detrital N.
Estuaries vary widely in depth, light attenuation, resuspension rates and the composition of both catchment and marine nitrogen loads. It is not surprising that we do not find a simple relationship between TN load, flushing rate and chlorophyll. We have used a simple one-box steady-state model here to understand better how these factors control the fate and composition of nitrogen in idealized estuaries. This model can be applied to individual estuaries, to understand the cycling of nitrogen, and predict response to changes in loads, and we have implemented a version of the steady-state 1-box model in Java, for this purpose. However, many estuaries are not well-approximated by a single well-mixed compartment, and the representation of physical transport by a single flushing rate has significant limitations. We have therefore implemented this biogeochemical model within a more realistic physical framework for application to real estuaries. The physical transport model is based on an inverse approach, described in Chapter 5. The combined model, and its application to a number of test cases, is presented in Chapter 6.
This chapter describes a simple inverse model that provides the transport field for generic estuarine transport or eutrophication models. The chapter first describes the "Hansen-Rattray" scheme of estuary classification and indicates the types of models that are required for different types of estuaries. We then describe a number of possible models that could be used for simulating transport fields in estuaries, prior to selection of the "one-dimensional n-layer hybrid model" described below. The chapter concludes by describing some specific features of the one-dimensional n-layer hybrid model implemented for this study. This chapter is quite technical, and may be skipped by those uninterested in physical modelling of estuaries.
Probably the most widely used scheme for estuary classification is that due to Hansen and Rattray (1966) (later developed by Scott (1993) and Winter (1973), for example). This scheme, although developed for normal estuaries where freshwater inflow exceeds evaporation, may also be used for the opposite case (inverse estuaries) which are common in Australia at certain times of the year (e.g. Lennon et al, 1987). The Hansen and Rattray scheme relies on two dimensionless parameters, which may be chosen from either of two parameter pairs. The first pair involves local observations of the velocity and salinity stratification in the estuary (Us/Uf and dS/So), where Us is the surface current, Uf the sectionally-averaged current, dS is the top-to-bottom salinity difference and So is sectionally-averaged salinity, and all quantities have been tidally-averaged. When these observations are not available, a pair of "external" dimensionless variables may be used, a "densimetric Froude number" and the ratio between Uf and the tidal current. In this latter case, only observations of freshwater flow (including precipitation and evaporation, if appropriate), the tidal velocity and the estuary geometry are required. An important output from the Hansen and Rattray classification is a value of the diffusive fraction, n, which describes the relative importance of external mixing processes (e.g. tidal and wind mixing) and those due to the buoyancy-driven circulation of the estuary. The diffusive fraction is formally defined as the ratio between the upstream flux of salt attributable to external mixing processes and the downstream flux of salt attributable to the river flow. A strongly stratified estuary driven predominantly by buoyancy forcing is characterised by n » 0, while an embayment driven mainly by tides and winds is characterised by n » 1.
The value of the diffusive fraction, n, estimated by the Hansen and Rattray classification provides a useful indication of the type of physical model to be applied to a given estuary. For low values of n, stratification is important and a layered model is required. As n approaches unity, a vertically well-mixed model such as a horizontally one-dimensional or single box model becomes more appropriate. Hybrid models combining the features of these one- and two-layer models are described below.
In this report, the smallest spatial entity is termed a cell. Cells are arranged horizontally in columns and vertically in layers. Each column and each layer is defined by a corresponding index. A specific cell is defined by a column index and a layer index.
A simple model for deriving a "plausible" velocity field in an estuary was described by Hunter (1977). The model required current velocities observed at the lateral boundaries of the estuary and involved a solution of Laplace's equation on a two- or three-dimensional grid (the former representing a vertical slice), yielding a modified form of the velocity potential (termed the "pseudo-potential"). Flow fields involving a velocity potential are normally irrotational and are therefore not appropriate for describing the vertically sheared currents found in an estuary. However, the pseudo-potential technique used a scaling of the axes prior to solution for the velocity potential, thereby allowing the solution to have a finite current shear. A major disadvantage of this model, however, is that it can only simulate the current velocity and can provide no information on turbulent diffusive transports. It was therefore rejected for use in the present application.
A schematic elevation view of the single-layer model is shown in Figure 5.1. Tracer (e.g. salinity) concentrations are defined as averages over each cell. Fluxes of water are defined at cell faces. At each face are defined two fluxes in opposite directions, say qi,i+1 and qi+1,i; the flux is directed from the cell indicated by the first subscript to the cell indicated by the second subscript. The advective and diffusive fluxes from cell i to cell i+1 are given by qi,i+1-qi+1,i and qi,i+1+qi+1,i, respectively.
The tracer flux between cells i and i+1 is given by Ci qi,i+1- Ci+1 qi+1,i.
The above fluxes may be determined by using a conservative tracer and a knowledge of the time-averaged longitudinal flux of tracer within the system. The most common tracer used in an estuary is salt, in which case the time-averaged longitudinal flux of tracer is zero. Therefore, replacing C with S to indicate salinity
| Si qi,i+1 - Si+1 qi+1,i = 0 | 5.1 |
The total flux of water is given by the river flow, R, so that
| qi,i+1-qi+1,i = R | 5.2 |
Equations 5.1 and 5.2 yield
| qi,i+1 = R Si+1 / (Si+1-Si) | 5.3 |
and
| qi+1,i = R Si / (Si+1-Si) | 5.4 |
Equations 5.3 and 5.4 may then be used to simulate the transport of another tracer (C) within the system. For example, the time-dependent concentration of a conservative tracer, subject to a set of sources, Qi in the i-th cell, is given by
| d Ci / dt = Ci-1 qi-1,i - Ci (qi,i-1 + qi,i+1) + Ci+1 qi+1,i + Qi | 5.5 |
where t is time, and the steady-state solution is given by
| Ci-1 qi-1,i + Ci+1 qi+1,i - Ci (qi,i-1 + qi,i+1) + Ci+1 qi+1,i = - Qi | 5.6 |
Equation 5.6 may be solved using a tridiagonal matrix solver.
This model, and the ones to be described in the following sections, are called "inverse" models.

|
| Figure 5.1. Structure of interior cells of single-layer model. |
This model was first described by Pritchard (1969). The schematisation of the model, which is essentially two one-layer models stacked vertically, is shown in Figure 5.2. In order to provide a system that was exactly determined, Pritchard assumed that horizontal diffusive processes were negligible, such that there is only one exchange flux at each vertical interface. This requires that the dominant mechanism for horizontal exchange is the buoyancy-driven estuarine circulation, rather than other processes such as turbulent tidal mixing (i.e. that the diffusive fraction described above is small).
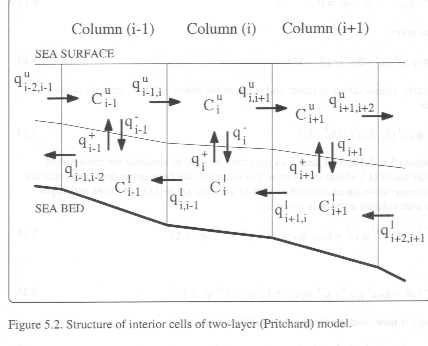
|
| Figure 5.2. Structure of interior cells of two-layer (Pritchard) model. |
As in the previous section, the exchange fluxes may be determined using a conservative tracer such as salt. The following is a slightly different formulation from that of Pritchard, in that upstream differencing is used instead of central differencing in order to constrain spurious oscillations in the final tracer solutions. A zero total horizontal salt flux requires that
| Siu qi,i+1u - Si+1l qi+1,il = 0 | 5.7 |
The total flux of water is given by the river flow, R, so that
| qi,i+1u - qi+1,il = R | 5.8 |
Equations 5.7 and 5.8 yield
| qi+1,il = R Siu / (Si+1l - Siu) | 5.9 |
and
| qi,i+1u = R Si+1l / (Si+1l - Siu) | 5.10 |
Conservation of tracer and water at the upper cell with column index i yields
| Si-1u qi-1,iu - Siu qi,i+1u + Sil qi+ - Siu qi- = 0 | 5.11 |
and
| qi-1,iu - qi,i+1u + qi+ - qi- = 0 | 5.12 |
which gives
| qi+ = qi-1,iu (Siu - Si-1u) / (Sil - Siu) | 5.13 |
Similarly, conservation or tracer and water at the lower cell with column index i yields
| qi- = qi+1,il (Sil-Si+1l) / (Siu - Sil) | 5.14 |
Equations 5.9, 5.10, 5.13, and 5.14 may then be used to simulate the transport of another tracer (C) within the system. For example, the time-dependent concentration of a conservative tracer, subject to a set of sources, Qil and Qiu in lower and upper cells with column index i, is given by
| d Cil / dt = - Cil qi,i-1l + Ci+1l qi+1,il - Cil qi+ + Ciu qi- + Qil | 5.15 |
and
| d Ciu / dt = Ci-1u qi-1,iu - Ciu qi,i+1u + Cil qi+ - Ciu qi- + Qiu | 5.16 |
where t is time, and the steady-state solution is given by
| - Cil qi,i-1l + Ci+1l qi+1,il - Cil qi+ + Ciu qi- = - Qil | 5.17 |
and
| Ci-1u qi-1,iu - Ciu qi,i+1u + Cil qi+ - Ciu qi-= - Qiu | 5.18 |
Equations 5.17 and 5.18 may be solved using a banded matrix solver.
It should be noted that equations 5.9, 5.10, 5.13 and 5.14 are problematic when the salinity becomes uniform over depth or when the salinity becomes zero. An alternative technique is to solve the steady-state conservation equations for salt and water for each cell:
| -Sil qi,i-1l + Si+1l qi+1,il - Sil qi+ + Siu qi- = 0 | 5.19 |
| Si-1u qi-1,iu - Siu qi,i+1u + Sil qi+ - Siu qi- = 0 | 5.20 |
| - qi,i-1l + qi+1,il - qi+ + qi- = 0 | 5.21 |
| qi-1,iu - qi,i+1u + qi+ - qi- = 0 | 5.22 |
using a robust matrix solver such as singular value decomposition (SVD, e.g. Press et al, 1986). For a system with N columns, there are 4N equations and 4N unknown variables, assuming appropriate boundary conditions are defined. It should be noted that the conservation equations for water may be derived from the equivalent equations for salt by setting the salinity to unity.
The one-dimensional two-layer (Pritchard) model described in the previous sub-section suffers from the disadvantage that it only performs well with estuaries that have a low diffusive fraction. If the diffusive fraction is high, the Pritchard model "attempts" to parameterise the horizontal turbulent exchange by increasing the vertical shear in the horizontal exchange fluxes. These large horizontal fluxes are not a good approximation of turbulent exchange and in such cases the use of the single-layer model described earlier is preferable. However, an alternative solution which incorporates the benefits of both models is to include horizontal turbulent exchanges in the two-layer model. This model (the "hybrid model") involves two extra unknown variables for each of the N columns, so that the problem is underdetermined with 4N equations and 6N unknown variables. Such underdetermined problems are now common in geophysics, and may be solved by using additional information such as the incorporation of extra equations or the application of smoothness constraints. A common technique is to use SVD, which yields a "minimum length" solution (i.e. a solution vector with a minimum sum of squares). This method requires prior weighting of the conservation equations (it is common to apply more weight to the conservation equations for water) and of the dependent variables (for example, it is clear that vertical exchanges should be weighted differently from horizontal exchanges).
The schematisation of the two-layer hybrid model is shown in Figure 5.3. The steady-state conservation equations for salt and water are:
| Si-1l qi-1,i l - Sil qi,i-1l - Sil qi,i+1l + Si+1l qi+1,il - Sil qi+ + Siu qi- = 0 | 5.23 |
| Si-1u qi-1,iu - Siu qi,i-1u - Siu qi,i+1u + Si+1u qi+1,iu + Sil qi+ - Siu qi- = 0 | 5.24 |
| qi-1,il - qi,i-1l - qi,i+1l + qi+1,il - qi+ + qi- = 0 | 5.25 |
| qi-1,iu - qi,i-1u - qi,i+1u + qi+1,iu + qi+ - qi- = 0 | 5.26 |
The exchange fluxes, ql, qu, q+ and q-, may be derived from the salinity field using appropriate weighting of the equations 5.23 5.26 and fluxes, suitable boundary conditions and a matrix solver such as SVD. It should be noted that this hybrid model reverts to the "upstream difference" Pritchard model with the addition of the equations qi-1,il=0 and qi,i-1u = 0 for all i. Alternatively, the original "centred difference" model of Pritchard (1969) may be obtained with the addition of the equations qi-1,il + qi,i-1l = 0 and qi-1,iu +qi,i-1u =0 for all i.
The exchange fluxes may then be used to simulate the transport of another tracer (C) within the system. For example, the time-dependent concentration of a conservative tracer, subject to a set of sources, Qil and Qiu in lower and upper cells with column index i, is given by
| d Cil / dt = Ci-1l qi-1,il - Cil qi,i-1l - Cil qi,i+1l + Ci+1l qi+1,il -Cil qi+ + Ciu qi- + Qil | 5.27 |
and
| d Ciu / dt = Ci-1u qi-1,iu - Ciu qi,i-1u - Ciu qi,i+1u + Ci+1u qi+1,iu + Cil qi+ - Ciu qi- + Qiu | 5.28 |
where t is time, and the steady-state solution is given by
| Ci-1l qi-1,il - Cil qi,i-1l - Cil qi,i+1l + Ci+1l qi+1,il - Cil qi+ + Ciu qi- = - Qil | 5.29 |
and
| Ci-1u qi-1,iu - Ciu qi,i-1u - Ciu qi,i+1u + Ci+1u qi+1,iu + Cil qi+ - Ciu qi- = - Qiu | 5.30 |
Equations 5.29 and 5.30 may be solved using a banded matrix solver.

|
|
Figure 5.3. Structure of interior cells of two-layer hybrid model. |
The two-layer hybrid model described in the previous section may be extended by considering an arbitrary number of layers. The one-layer and two-layer models are then just special cases of this generic model.

|
|
Figure 5.4. Structure of interior cells of n-layer hybrid model. |
The schematisation of the n-layer hybrid model is shown in Figure 5.4. Column and layer indices are given by i and j, respectively. The steady-state conservation equations for cell (i,j), for salt and water, are:
| Si-1j qi-1,ij - Sij qi,i-1j - Sij qi,i+1j + Si+1j qi+1,ij + Sij-1 qij-1,j - Sij qij,j-1- Sij qij,j+1 + Sij+1 qij+1,j = 0 | 5.31 |
and
| qi-1,ij - qi,i-1j - qi,i+1j + qi+1,ij + qij-1,j - qij,j-1 - qij,j+1 + qij+1,j = 0 | 5.32 |
The exchange fluxes, qi,i+1j, qi+1,ij, qij,j+1 and qij+1,j may be derived from the salinity field using appropriate weighting of the equations 5.31, 5.32 and fluxes, suitable boundary conditions and a matrix solver such as SVD.
The exchange fluxes may then be used to simulate the transport of another tracer (C) within the system. For example, the time-dependent concentration of a conservative tracer, subject to a set of sources, Qij, in cells with column index i and layer index j, is given by
| d Cij / dt = Ci-1j qi-1,ij - Cij qi,i-1j - Cij qi,i+1j + Ci+1j qi+1,ij + Cij-1 qij-1,j - Cij qij,j-1- Cij qij,j+1 + Cij+1 qij+1,j + Qij | 5.33 |
where t is time, and the steady-state solution is given by
| Ci-1j qi-1,ij - Cij qi,i-1j - Cij qi,i+1j + Ci+1j qi+1,ij + Cij-1 qij-1,j - Cij qij-1,j - Cij qij,j+1 + Cij+1 qij+1,j = - Qij | 5.34 |
Equation 5.34 may be solved using a banded matrix solver.
The conservation equations and fluxes require weighting prior to solution by SVD (the technique chosen for the present model), for the following reasons:
1) Conservation equations in which we have most confidence (e.g. conservation of water) should generally be weighted higher than the others. Further, if the resultant fluxes are to be used in some form of transport model, then it is imperative that they satisfy volume conservation, requiring that the water conservation equation be solved exactly. The problems presently being considered are generally always underdetermined so that we can solve all the conservation equations exactly, and weighting of the equations prior to SVD is strictly unnecessary. However, accuracy constraints due to round-off error make weighting of the equations advisable. In the present model, the salt conservation equations are weighted by a factor of 0.03, in order to make them of the same order as the water conservation equations.
2) For underdetermined problems such as these, SVD yields a minimum length solution (i.e. one with a minimum sum of squares), which tends to give components of similar magnitudes. Generally, the horizontal and vertical fluxes in a cell-based model will be systematically different, dependent on the aspect ratios of the cells (e.g. for a two-layer model, increasing the horizontal cell dimension increases the vertical fluxes but does not affect the horizontal fluxes). The present model therefore allows a single scalar weighting to be applied to the vertical fluxes prior to SVD. This weighting must of course be applied in the inverse sense to the resultant solution vector to obtain the actual water fluxes. The flux weighting also needs to be considered carefully in cases where the fluxes are poorly defined, such as in the upper reaches of the estuary where the water is fresh. In such regions, there is no salt to act as a tracer and the fluxes are only constrained by water conservation. Since the minimum length solution tends to yield component values of similar magnitude, it may often be better to solve for the water velocity rather than the water flux, so as to minimise the variation of water velocity in the vertical. This option is implemented in the present model by using weights based on the normalised cross-sectional area of the vertical face appropriate to each flux.
The n-layer hybrid model of Section 5.3.6 may be used to derive the diffusive fraction defined earlier. For the vertical face defined by the column indices (i,i+1) (see Figure 5.4), the total downstream flow (R) is given by
| R = Sj=1n qi,i+1j - qi+1,ij | 5.35 |
which is assumed to be distributed among the layers according to the weight, wj, so that the "river" flow in each layer is R wj and
| Sj=1n wj = 1 | 5.36 |
The total flows qi,i+1j and qi+1,ij may therefore each be separated into a part due to the river flow [I] and the remainder [II]:
| qi,i+1j = R wj / 2 [I] + (qi,i+1j - R wj/2) [II] | 5.37 |
| qi+1,ij = - R wj / 2 [I] + (qi+1,ij + R wj / 2) [II] | 5.38 |
The downstream salt flux may now be separated into three parts:
1. T, a part due the river flow (term I),
2. A, an advective part due to the remainder (term II), and
3. D, a diffusive part due to the remainder (term II),
(the separation of the "advective" and "diffusive" parts (A and D) being based on terms involving (Sij+Si+1j) and (Sij - Si+1j), respectively):
| T = Sj=1n R wj (Sij + Si+1j) / 2 | 5.39 |
| A = Sj=1n (qi,i+1j - qi+1,ij - R wj) (Sij + Si+1j) / 2 | 5.40 |
| D = S j=1n (qi,i+1j + qi+1,ij) (Sij - Si+1j) / 2 | 5.41 |
From equations 5.39 to 5.41,
| T + A + D = S j=1n qi,i+1j Sij - qi+1,ij Si+1j | 5.42 |
the total downstream salt flux in the estuary, which is zero.
The diffusive fraction, n
, is defined by - D/T (the minus sign making the result positive), or
| n = - S j=1n (qi,i+1j + qi+1,ij) (Sij - Si+1j) / (R S j=1n wj (Sij + Si+1j)) | 5.43 |
In the present implementation of the model, wj is approximated by 1/n, so that
| n » - S j=1n (qi,i+1j + qi+1,ij) (Sij - Si+1j) / (R S j=1n (Sij + Si+1j)) | 5.44 |
Transport or ecological models, using simple numerical time-stepping schemes to solve equations such as Equation 5.33, often show undesirable oscillations in the solution. A common way of overcoming this problem is through the use of "upstream differencing" (e.g. Vreugdenhil, 1989) which adds sufficient extra diffusion to suppress the oscillations. The use of this technique in the present implementation of the model is as follows. The exchange fluxes (which may be either horizontal or vertical) between any two cells labelled a and b are defined by the subscript pairs (a,b) and (b,a), and the fluxes derived from the inverse model are denoted by Qa,b and Qb,a. Using the upstream differencing scheme, these fluxes are replaced by new ones Q'a,b and Q'b,a prior to use in the transport model:
| Q'a,b = Qa,b + d | 5.45 |
and
| Q'b,a = Qb,a + d | 5.46 |
where
| d = | min (Qa,b ,Qb,a,0) | | 5.47 |
The fluxes are therefore modified if either Qa,b or Qb,a is negative, in which case, one of the new fluxes Q'a,b or Q'b,a is defined to be zero.
Although the derivation of fluxes by the inverse model is based on an assumption of steady state, it is often required that the corresponding transport or ecological model be time-varying. In the present modelling system the following simple approximation is used to derive time-varying velocity fields.
The complete set of fluxes for one realisation of the inverse model (i.e. qi,i+1j and qij,j+1) is represented by the vector Qkl, where k and l indicate the location and realisation of the flux, respectively. For each realisation, l, there is a corresponding observed river flow, Rl. Qkl and Rl are ordered so that Rl increases monotonically with l. At any given time, t, during a run of a transport or ecological model, the fluxes are derived by linear interpolation of Qkl based on Rl and the river flow R(t). Therefore, if Rl < R(t) £
Rl+1, the interpolated fluxes (Qkl)int are derived from:
| w1 = (Rl+1 - R(t)) / (Rl+1 - Rl ) | 5.48 |
| w2 = (R(t) - Rl ) / (Rl+1 - Rl ) | 5.49 |
| (Qkl)int = w1 Qkl + w2 Qkl+1 | 5.50 |
Since the original fluxes Qkl conserve volume, so too must the interpolated fluxes (Qkl)int, due to the linearity of the conservation equations.
The main approximations in this technique are both related to time dependence, and are as follows:
1. the inverse technique used to obtain the fluxes Q involves the assumption that the salinity field is in a steady state, and
2. the technique described in Equations 5.48 to 5.50 involves the assumption that the exchange fluxes associated with a time-varying river flow are the same as the fluxes associated with a steady river flow of the same magnitude.
Both (1) and (2) are essentially equivalent to the assumption that the river flow changes on a time scale of the same order as, or longer than, the flushing time of the estuary (which itself depends on the river flow). The validity of this assumption will depend on the properties of the particular catchment and estuary.

|
|
Figure 5.5. Derwent Estuary: observed salinity under low flow (62 m3 s-1) conditions. |
As an example, this technique has been applied to the Derwent Estuary, Tasmania. The hybrid 2-layer inverse method was applied to salinity distributions observed under periods of low flow (62 m3 s-1) and of high flow (221 m3 s-1). The results were then used to force a transport model of the salinity, starting with the river flow and salinity appropriate to the "low flow" condition and increasing the river flow linearly to the "high flow" value over a period of 106 seconds (11.6 days, which is roughly the same as the flushing time of the estuary). Figure 5.5 shows the salinity observed during the "low flow" period. The spatial separation of each column in this model is roughly 2 km, the river enters at the left-hand side and the open boundary is at the right-hand side. Figure 5.6 shows both the simulated salinity at the end of the run and the observed "high flow" salinity. The agreement between observations and predictions is good, especially for the upper layer. A major contributor to the comparative smoothness of the predicted salinity in the lower layer is numerical diffusion, which is a result of the upstream differencing technique used (see above) rather than of the method used to simulate time-dependence.

|
|
Figure 5.6. Derwent Estuary: observed and simulated salinity under high flow (221 m3 s-1) conditions. |
In this chapter, we describe the application of a simple spatially-resolved biogeochemical model to three estuaries. The model (the Simple Estuarine Eutrophication Model or SEEM) essentially represents an implementation of the simple nutrient cycling model described in Section 4 within the n-layer hybrid transport model described in Chapter 5.
There are only two minor changes to the 1-box biogeochemical model analysed in Chapter 4, defined by Eq 4.1 4.11. First, to allow for multiple vertical layers, we have changed the formulation for light-limited growth. We now compute the average light intensity within each layer k, lying between heights zk-1 and zk, and having thickness Hk = zk zk-1, by
|
I(zk-1) = I(zk) . exp(-K.Hk) |
6.1 |
|
<I>k = (I(zk) I(zk-1)) / (K.Hk) |
6.2 |
and then compute hI for layer k as:
|
hI = (1. exp(-<I>k / IK)) |
6.3 |
This means that the user must now specify the saturation light intensity IK .
Secondly, we now compute the suspended fraction s for each cell and tracer separately as follows. We specify a sinking rate w (m d-1) for each particulate constituent, and a resuspension rate Su with units of d-1 for bottom sediments in each cell. For bottom cells, the suspended fraction is just
|
s = Su . H / (Su.H + w). |
6.4 |
For other cells, the model geometry specifies plan areas for the top and bottom of the cell, Ak and Ak-1, and computes the cell volume Vk = H.(Ak-1+ Ak)/2. This implies a bottom sediment area equal to Ak Ak-1. The sinking flux of tracer C from cell k+1 to cell k is given by w.C.Ak. The suspended fraction is then given by
|
s = Su . Vk / (Su .Vk + w . (Ak Ak-1) ) |
6.5 |
The model is implemented in JAVA with a user interface which supports run management and output visualisation. This package is documented in Parslow et al (1999). The model has been implemented as a dynamical model, and will accept time series of forcing variables (river runoff, loads and boundary conditions). However, the test cases here have all been analysed at steady-state.
The Derwent River estuary in Hobart is a drowned river valley, moderately deep, draining a large catchment, with (by Australian standards) consistent runoff. Much of the catchment is undisturbed, although there is agricultural development in the downstream parts of the catchment. The city of Hobart sits astride the Derwent, and the estuary receives nutrient loads from a large number of small Wastewater Treatment Plants (WTPs), and some industrial sources.
Data from three recent major field surveys have been used here. CSIRO conducted a series of extensive near-synoptic spatial surveys of physical and chemical properties on an intensive sampling grid as part of the CSIRO Coastal Zone Program. The salinity data from those surveys have been used as input to the inverse model, to estimate physical exchanges over a range of river flows.
The Tasmanian Department of Environment and Land Management conducted two major studies of the Derwent Estuary in 1994 and 1996. Physical, chemical and biological properties were sampled approximately monthly at a series of locations along the length of the estuary, with some additional sampling in the side embayments. DELM has kindly made available data collected in May 1994, and January, February, April and July 1996. Summaries of these data have been published in two technical reports (Coughanowr, 1995, 1997), which also identify the principal industrial and WTP point sources, and provide estimates of nitrogen loads from these sources. (These reports also provide an excellent general description of the estuary and catchment.)
The Derwent is relatively deep and, given the high runoff and low tidal amplitude, represents a classic example of a Pritchard-type salt-wedge estuary. The estuary can be divided length-wise into three sections (Fig. 6.1). The upper estuary from New Norfolk down to just above Bridgewater, a distance of about 13 km, is relatively narrow, and dominated by river flow. The middle estuary, from just above Bridgewater down to Hobart, is of order 1 km wide, and includes a number of shallow side embayments. The lower estuary, from Hobart to the Iron Pot, is much broader (order 5 km) and generally marine-dominated. One might expect diffusive exchanges to be more important in the lower estuary.
The estuary has been modelled here using a two-layer hybrid model, with 31 columns. This relatively high resolution along-stream is justified by the high spatial resolution of the field surveys, and the large number of point sources distributed along the estuary. The lengths, mean depths, plan areas and shape factors for model cells were derived from a fine-resolution bathymetry and model grid prepared by CSIRO (Hunter, pers. comm.).
The Derwent River discharge is by far the dominant freshwater input into the estuary. The river is dammed and used to generate hydro-electricity, so the discharge is strongly regulated. While flow may drop to about 20 m3 s-1 for brief periods, it is typically greater than 50 m3 s-1, and peak discharge can reach 300 m3 s-1 (Coughanowr, 1995).

|
|
Fig. 6.1. Map of Derwent estuary, showing sampling stations in CSIRO surveys. |
| (original size image) |
Salinity data from the CSIRO surveys were averaged to the model geometry and used with the inverse model described previously to estimate horizontal and vertical exchanges at 4 river flows: 65, 95, 164 and 218 m3 s-1. Exchanges for other flow rates corresponding to the water quality data sets described below were estimated by interpolation, as described in Chapter 5.
Coughanowr (1995, 97) provides estimates of average DIN loads from the WTPs and industrial sources along the Derwent. These loads have been assumed to be constant within years. Estimates of organic N loads from WTPs were not available, but these are thought to be low, as most of the plants carry out secondary treatment. We have assumed a labile organic N load from each WTP equal to 10% of the DIN load, but this makes little difference to model predictions. The point source loads in 1996 are shown in Table 6.1.
Table 6.1. Location, distance downstream from New Norfolk, and magnitude of DIN and DET loads for Derwent Estuary point sources. | |||
|---|---|---|---|
Location |
Distance downstream |
DIN Load |
DET Load |
New Norfolk |
0 |
939 |
94 |
ANM Paper Mill |
3 |
21 |
1600 |
Bridgewater |
20 |
685 |
69 |
Cameron Bay |
28 |
1671 |
167 |
Macquarie Point |
32 |
2609 |
261 |
Prince of Wales Bay |
32 |
3202 |
320 |
East Risdon |
32 |
48 |
5 |
Pasminco EZ |
34 |
412 |
0 |
Selfs Point |
36 |
913 |
91 |
Rosny |
39 |
2844 |
284 |
Sandy Bay |
42 |
1128 |
113 |
Taroona |
47 |
310 |
31 |
Blackmans Bay |
55 |
1088 |
109 |
The river load corresponding to each survey was estimated by multiplying the measured concentrations of DIN and organic N in freshwater at New Norfolk by the river flow at the time of the survey. Standard measurements do not distinguish labile and refractory organic N. The river load of organic N was all assigned to the refractory component (see discussion below).
As discussed above, the SEEM model has been used here as a steady-state model and run to steady-state with river flows, physical exchanges and loads corresponding to the DELM 1994 and 1996 surveys for which data were available. The 1994 surveys sampled more stations along estuary, and sampled top and bottom layers in almost all locations. Unfortunately the May 1994 survey did not measure Chl a or total (organic) N. The 1996 surveys sampled fewer stations, and sampled only the surface layer at most stations, but did measure Chl a and total N at almost all stations.
We first present comparisons of predicted and observed surface DIN, Chl a and TN for the 1996 surveys. These predictions all use a "standard" parameter set (Table 6.2), except that the maximum phytoplankton growth rate and grazing loss rate were reduced from the summer values in Table 6.2 to winter values of 1.0 d-1 and 0.3 d-1 respectively in April and July.
The background light attenuation in Table 6.2 is rather high, and is based on observed Secchi depths of around 3 m. This is due to the high concentrations of CDOM in the river runoff. Light limitation plays a critical role in the estuary, as we discuss below.
Table 6.2. "Standard" parameter set used in Derwent simulations (see text). | |||
|---|---|---|---|
Symbol |
Description |
Units |
Value |
mmax |
Maximum phytoplankton growth rate |
d-1 |
1.5 |
KN |
Half-saturation constant for phytoplankton growth on DIN |
mg N m-3 |
10 |
IK |
Light saturation intensity |
W m-2 |
10 |
m0 |
Background constant phytoplankton loss rate |
d-1 |
0.1 |
m1 |
Maximum grazing loss rate |
d-1 |
0.6 |
KP |
Phytoplankton biomass corresponding to maximum grazing loss rate |
mg N m-3 |
20 |
fDET |
Fraction of grazing losses to labile detritus |
0.5 | |
fREF |
Fraction of labile detritus to refractory detritus |
0.1 | |
rDET |
Breakdown rate of labile detritus |
d-1 |
0.1 |
rREF |
Breakdown rate of refractory detritus |
d-1 |
0.01 |
EDENmax |
Maximum denitrification efficiency |
0.6 | |
R0 |
Sediment respiration rate at which EDEN = 0. |
mg N m-2 d-1 |
250 |
K0 |
Background light attenuation |
m-1 |
0.7 |
k*PHY |
Specific light attenuation for phytoplankton |
m2 (mg N)-1 |
0.0035 |
k*DET |
Specific light attenuation for labile detritus. |
m2 (mg N)-1 |
0.0035 |
k*REF |
Specific light attenuation for refractory organic N |
m2 (mg N)-1 |
0.0009 |
wPHY |
Sinking rate of phytoplankton |
m d-1 |
0 |
wDET |
Sinking rate of labile detritus |
m d-1 |
1 |
wREF |
Sinking rate of refractory organic N |
m d-1 |
0 |
Note that the sinking rate of refractory organic N is set to zero, so that this pool is effectively treated as DON rather than PON.
The January 1996 survey corresponds to a period of low river flow (50 m3 s-1), and correspondingly low river loads. The model reproduces quite well the observed surface layer TN throughout the estuary, and the levels of surface DIN in the marine half of the estuary (Fig. 6.2). However, the model overpredicts DIN in the upper estuary. While the model predicts a phytoplankton bloom of about the right magnitude, it is displaced upstream about 10 km from the observed bloom. Note that the observed Chl a is quite low in the upper estuary, and so the model's overprediction of DIN there cannot be blamed on an underprediction of phytoplankton uptake.
The February 1996 survey corresponds to a period of moderate river flow (100 m3
s-1), and moderate loads. The model predicts a phytoplankton bloom displaced to the marine end of the estuary, and reproduces the observed Chl a of about 6 mg m-3 there quite well, although it fails to predict an observed peak of 8 mg Chl a m-3 around 45 km (Fig. 6.3). The model overpredicts surface layer DIN in the upper and mid-estuary. The observed DIN levels show a pronounced minimum around 15 km which the model completely fails to capture. Again, this occurs in a region where observed chlorophyll is very low.
The April 1996 survey occurred at a time of high river flow (about 200 m3 s-1), and consequently very high loads. In order to reproduce the observed behaviour, it was necessary to reduce mmax and m1 to 1 and 0.3 d-1. The model reproduces the TN distribution, and captures quite well a moderate phytoplankton bloom of about 2 mg Chl a m-3 displaced to the marine end of the estuary (Fig. 6.4). It also reproduces very well the moderate levels of Chl a measured in the mid-estuary. Predicted DIN levels also show reasonable agreement with observations, although the model fails to predict a sharp DIN peak at 40 km.
The July 1996 survey occurred during a period of moderate river flow (90 m3 s-1), and is notable for the high marine boundary concentrations of nitrate (DIN) associated with winter mixing on the adjacent continental shelf. The model reproduces DIN well in the lower estuary, but overpredicts DIN in the middle estuary (Fig. 6.5). Predicted maximum chlorophyll levels of 1.5 mg Chl a m-3 are in good agreement with observations, although the predicted peaks are displaced upstream and downstream of the observed peak. The model in July was run with reduced "winter" values for mmax and m1, and a reduced surface light intensity.
The May 1994 survey coincided with a period of moderate river flow (80 m3 s-1). As noted above, Chl a and TN data were not collected, but the predicted and observed DIN in surface and bottom layers are shown in Fig. 6.6. The model reproduces the downstream DIN levels well, but again fails to reproduce the observed depletion of DIN in both layers around 15 km.

|
|
Fig. 6.2. Predicted (line) and observed (diamonds) concentrations of TN, DIN and Chl a vs distance downstream for January 1996. |
| (original size image) |
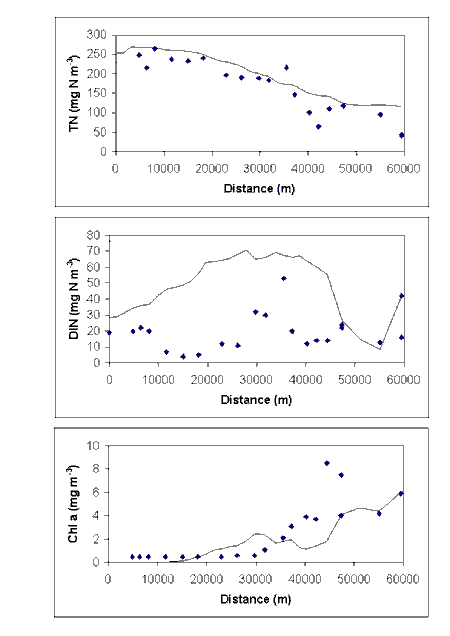
|
|
Fig. 6.3. Predicted (line) and observed (diamonds) concentrations of TN, DIN and Chl a vs distance downstream for February 1996. |
| (original size image) |

|
|
Fig. 6.4 Predicted (line) and observed (diamonds) concentrations of TN, DIN and Chl a vs distance downstream for April 1996. |
| (original size image) |

|
|
Fig. 6.5. Predicted (line) and observed (diamonds) concentrations of TN, DIN and Chl a vs distance downstream for July 1996. |
| (original size image) |

|
|
Fig. 6.6 Predicted (line) and observed (diamonds) concentrations of DIN in top and bottom layers vs distance downstream for May 1994. |
| (original size image) |
Overall, the model depicts the Derwent as a strongly light-limited system, where DIN is rarely fully utilised. Maximum phytoplankton biomass and DIN drawdown is predicted in summer, at times of maximum temperature and surface light intensity. The estuary is then able to support blooms of order 5 to 8 mg Chl a m-3, although phytoplankton growth is then in a delicate balance with flushing, and higher flow rates reduce chlorophyll levels and push blooms towards the estuary mouth. In winter, growth is strongly light-limited, and phytoplankton are unable to take advantage of the high levels of DIN supplied into the estuary from continental shelf waters.
The effect of background light attenuation K0 on phytoplankton biomass in the Derwent is shown in Fig. 6.7, which compares the predicted biomass in July for the standard run (K0 = 0.7 m-1) with that predicted for K0 = 0.1 m-1, a value more typical of shelf waters. The predicted biomass increases almost 10-fold to about 12 mg Chl a m-3, driven by the combination of local DIN loads and shelf nitrate.

|
|
Fig. 6.7. Predicted Chl a for July 1996 for background light attenuation K0 set to 0.7 m-1 (solid line, standard run) and 0.1 m-1 (dashed line). |
| (original size image) |
A common feature of all model-data comparisons is the model's failure to predict the observed strong drawdown of DIN in the upper estuary around 15 to 20 km. There must be a strong sink in this location, as it is subject to both surface loads from upstream and bottom layer loads from downstream. Both the observed and predicted levels of phytoplankton biomass are incapable of accounting for the observed DIN depletion. A possible explanation is that benthic plant communities distributed over the extensive shallow side embayments in this region of the river take up DIN. As the DIN appears to be removed from the system, it must be either buried as organic N, or lost to denitrification in sediments.
An alternative DIN sink is heterotrophic benthic denitrification. The river load of DIN is primarily nitrate, and the upper estuary has also been subject to very large loads of organic carbon from the ANM paper mill, which are known to have been deposited on the estuary bed around Bridgewater, creating anoxic mats. This could create ideal circumstances for denitrification of nitrate diffusing from the water column. The high light attenuation may also favour nitrification of ammonium in the bottom layer, allowing recycled ammonium and ammonium from WTPs advected upstream to enter this heterotrophic denitrification pathway.
Denitrification is represented in the model, but because flushing is relatively rapid, it contributes relatively little to the overall nitrogen balance. In January 1996, the period of lowest flushing and maximum phytoplankton production, switching off denitrification leads to only a 20% increase in predicted DIN and Chl a (Fig. 6.8).
Another way to switch off denitrification is to set the sinking rate of labile detritus to zero, as this prevents sedimentation, and hence benthic denitrification. However, as shown in Fig. 6.8, this results surprisingly in a decrease in DIN and Chl a. This is due to the interaction of sedimentation with the 2-layer estuarine circulation. Detritus sinking from the top layer into the bottom layer is advected upstream in the estuary, and recycled to DIN to be entrained again in the surface layer. This trapping of sinking particulates can considerably increase residence time in the estuary.

|
|
Fig. 6.8. Predicted DIN and Chl a for January 1996, for standard run (light solid line), denitrification set to zero (dashed line) and wDET = 0 (bold line). |
| (original size image) |
The two-layer estuarine circulation also has important implications for the location of point source loads. WTP outfalls into the Derwent are discharged into bottom waters. Fig. 6.9 shows the model predictions for January 1996, along with predictions for the same parameter set and loads, but with all point source loads discharged into surface waters. The predicted Chl a peak in the mid-estuary is reduced by almost 50%, simply because DIN discharging into the surface layer is flushed much more efficiently from the estuary.

|
|
Fig. 6.9. Predicted Chl a for January 1996, with all point source loads directed into bottom layer (solid line, standard run) or into top layer (dashed line). |
| (original size image) |

|
|
Fig. 6.10. Predicted DIN and Chl a for "January 1996" for a hypothetical single point source load of DIN (20 g N s-1) located in the bottom layer either 30 km (solid line) or 40 km (dashed line) from the head of the estuary. |
| (original size image) |
The effective flushing rate in any estuary increases towards the mouth, and the Derwent is no exception. This is illustrated with an entirely hypothetical case in Fig. 6.10, which shows DIN and Chl a fields for a single point source of DIN of 20000 mg N s-1 located either approximately 30 km or 40 km downstream, and injected into the bottom layer. The predicted Chl a peak increases from 2 to 11 mg Chl a m-3 as the location is shifted 10 km upstream. This reflects not only the reduced flushing rate, but also the increased time available for phytoplankton growth.
The Brunswick River estuary in northern New South Wales drains a catchment of about 218 km2, of which 50 to 75% has been cleared for grazing and agriculture (Eyre, 1997). The estuary also receives nutrient inputs from three WTPs, and is recognised as suffering from poor water quality.
The data used in this test case was collected in 1996 by Bradley Eyre as part of a study commissioned by the Byron Council and kindly made available as a test data set. Six surveys measured physical, chemical and biological variables at approximately 20 stations along the estuary (Eyre, 1997). The station locations were not fixed in space: instead samples were taken at approximately equal salinity intervals. Samples were collected in the freshwater just upstream of the estuary by volunteers to provide estimates of loads.

|
|
Fig. 6.11. Brunswick Estuary. |
| (original size image) |
The estuary (Fig. 6.11) is about 12 km from the head to the mouth. Only the main estuary channel has been modelled here. Two major tributaries, Simpson's Creek and Marshall's Creek, entering near the mouth have not been included (but see loads below). The estuary is generally narrow and quite shallow (typical depths of 2 to 4 m), so that the volume is low. The tidal amplitude is about 2 m, and this, combined with the shallow depth, means that the estuary is strongly mixed. Salinity profiles collected as part of the surveys show weak vertical gradients compared with horizontal gradients (Eyre, 1997), and the estuary is well-approximated by a 1-layer "diffusive" model, at least during the prolonged periods of low flow.
We have represented the estuary as a 1-layer diffusive model and divided the length of the estuary into 13 cells, each approximately 1 km long. Plan areas, depths and shape factors for these cells were supplied by Eyre, and based on local charts.
Eyre (1997) notes that runoff is generally low, with occasional episodes of very high runoff which flush the estuary fresh to the mouth. River flows preceding the 6 surveys conducted in 1996 ranged from 0.07 to 20.8 m3 s-1. The highest-flow event was sufficient to flush the estuary to the mouth. The inverse technique described in Chapter 5 was used to derive physical exchanges corresponding to the survey flows and salinity data.
We estimated loads from the river by multiplying concentrations at the furthest upstream station (salinities at these stations were generally < 1) by river flow. DON and PON concentrations were measured separately, and we treated the PON fraction as labile detritus and the DON fraction as refractory detritus. As discussed below, it was necessary to estimate P as well as N loads, and the organic P load was partitioned in a similar way (but see below).
The estuary receives direct inputs of effluent from WTPs at Mullumbimby, located about 3 km from the head of the estuary, and at Ocean Shores, about 3 km from the mouth. A third WTP, the Brunswick, is located on Simpson's Creek. Nutrient loads from this STP were injected directly into the downstream cell in the model. (As discussed below, this has negligible impact on water quality throughout most of the estuary.)
Estimates of monthly flows and concentrations of DIN, TN and TP from these WTPs are given by Eyre (1997). In the case of Ocean shores, both concentration and flow estimates vary month to month. In the case of Brunswick WTP, flows vary, but concentrations are fixed, while for Mullumbimby WTP both flows and concentrations are fixed, and presumably represent an annual average. It is not clear how constant these loads are in reality, or how accurate these load estimates are. We have assumed that the organic N load is all labile N, and that the TP load is 90% DIP and 10% labile organic P (again, see comments below).
The model has been applied at steady-state to 4 of the 6 surveys corresponding to low flow conditions: April (F = 0.235 m3 s-1), July (F = 0.44 m3 s-1), September (F = 0.07 m3 s-1) and December (F = 0.18 m3 s-1). We initially tried to model the estuary as an N-limited system, but it quickly became apparent that this was not appropriate.
Consider for example the September data collected at very low river flow. Using standard parameter values, the model predicts very high chlorophyll levels and DIN depletion throughout the estuary (Fig. 6.12). The model reproduces the TN distribution reasonably well, suggesting that the total nitrogen load and physical exchanges are approximately correct. However, the observations show very high levels of DIN and low values of chlorophyll by comparison.
A possible explanation for the observations is that phytoplankton are light-limited, as in the Derwent. Secchi depths reported by Eyre (1997) for September 1996 ranged from 1 to 2 m, corresponding to K values of about 1 to 2 m-1, so light attenuation is high. However, the water column is also very shallow, and so phytoplankton growth is not as sensitive to light attenuation. Even adopting a K0 of 4 m-1 in the model does not reduce the predicted bloom significantly. The bloom can be prevented by adopting unrealistically low phytoplankton growth rates, and the model then reverts to a low biomass, grazing controlled state. The predicted DIN levels then agree quite closely with observations (Fig. 6.13). This suggests that the estimated DIN loads are approximately correct, and that these are for the most part unutilised within the estuary.
Similar results are obtained for the other three surveys. While chlorophyll levels vary among surveys, phytoplankton consistently utilise a minor part of the DIN load. When phytoplankton growth is reduced to very low levels, the predicted TN and DIN concentrations generally agree reasonably well with observations. It seems questionable whether grazing control could really limit phytoplankton biomass so consistently, at such high levels of DIN, and in any case this would not explain the variation in chlorophyll from month to month.

|
| Figure 6.12. Predicted (line) and observed (diamonds) values of TN, DIN and Chl a, for the Brunswick estuary in September, using an N-limited model with standard parameter values. |
| (original size image) |

|
| Figure 6.13. Predicted (line) and observed (diamonds) values of TN, DIN and Chl a, for the Brunswick estuary in September, using an N-limited model with very low phytoplankton growth rates. |
| (original size image) |
The survey nutrient data suggest an alternative explanation. While DIN levels are very high, typically 300 to 500 mg N m-3, DIP levels are much lower, in the range 15 to 30 mg P m-3. This suggests that the system may be operating as P rather than N-limited. While the simple model presented here was not designed as a model of P-cycling and P-limitation, it can be adapted to model P by modifying model parameters appropriately. The parameter values have been modified assuming a Redfield N:P ratio of about 7 by weight. This means we assume that 1 mg Chla corresponds approximately to 1 mg phytoplankton P. A standard set of parameters used for the P simulations described below is given in Table 6.3.
Table 6.3. "Standard" parameter set used in Brunswick P-limited simulations (see text). | |||
|---|---|---|---|
Symbol |
Description |
Units |
Value |
mmax |
Maximum phytoplankton growth rate |
d-1 |
2.0 |
KN |
Half-saturation constant for phytoplankton growth on DIN |
mg P m-3 |
15-30 |
IK |
Light saturation intensity |
W m-2 |
10 |
m0 |
Background constant phytoplankton loss rate |
d-1 |
0.1 |
m1 |
Maximum grazing loss rate |
d-1 |
0.8 |
KP |
Phytoplankton biomass corresponding to maximum grazing loss rate |
mg P m-3 |
10 |
fDET |
Fraction of grazing losses to labile detritus |
0.5 | |
fREF |
Fraction of labile detritus to refractory detritus |
0.1 | |
rDET |
Breakdown rate of labile detritus |
d-1 |
0.1 |
rREF |
Breakdown rate of refractory detritus |
d-1 |
0.01 |
EDENmax |
Maximum denitrification efficiency |
0 | |
R0 |
Sediment respiration rate at which EDEN = 0. |
NA | |
K0 |
Background light attenuation |
m-1 |
2.0 |
k*PHY |
Specific light attenuation for phytoplankton |
m2 (mg P)-1 |
0.02 |
k*DET |
Specific light attenuation for labile detritus. |
m2 (mg P)-1 |
0.02 |
k*REF |
Specific light attenuation for refractory organic N |
m2 (mg P)-1 |
0.006 |
wPHY |
Sinking rate of phytoplankton |
m d-1 |
0 |
wDET |
Sinking rate of labile detritus |
m d-1 |
0 |
wREF |
Sinking rate of refractory organic N |
m d-1 |
0 |
Note that the maximum growth rate mmax and maximum grazing mortality rate m1 have been increased to 2.0 and 0.8 d-1 respectively to reflect warmer subtropical conditions. The phytoplankton biomass corresponding to maximum grazing mortality rate is set to 10, which is about 3 times larger in P-equivalents than the value used in the Derwent simulations. The half-saturation constant for nutrient-limited growth is set to 15 or 30 mg P m-3, or about 0.5 to 1 mM. These values are discussed further below. Finally, the specific light attenuation coefficients have been scaled for P rather than N.
Fig. 6.14 shows predicted and observed TP, DIP and Chl a for the very low flow conditions in September, using this standard parameter set, with KN = 15 mg P m-3. The agreement is quite good. However, in order to obtain this agreement, the TP load from Mullumbimby WTP had to be reduced by a factor of 10! Note that the agreement between predicted and observed TP, and the above agreement between predicted and observed TN (and salinity courtesy of the inverse model), shows that the model is exporting the correct amount of phosphorous.
"Denitrification" is turned off in adapting the model for P, and the model does not have an internal P sink. It is possible that the estimated P load from the WTP is correct, but that this load is lost to an internal sink (ie sequestered in the sediments) rather than exported. However, given the reasonable agreement in the predicted and observed long-estuary distribution of TP, that sequestration would have to occur in the immediate vicinity of the source. This could occur through adsorption of DIP onto sediment, and subsequent settling.
An alternative explanation is that the Mullumbimby WTP load given by Eyre (1997) over-estimates the effective delivery of P to the estuary. The effluent is discharged into a pond, and thence into the estuary. The pond is subject to intense algal blooms, which at times "spill over" into the estuary (Eyre, pers comm). It is possible that, under very low flow conditions, P is effectively trapped in the pond, which acts to provide partial tertiary treatment.
Model-data comparisons for the other surveys support this latter interpretation. During July (the highest river flow modelled), the model reproduces TP, DIP and Chl a reasonably well (Fig. 6.15) without any reduction in the estimated P load. Note that the increased P load results in much higher predicted and observed phytoplankton biomass. The model fails to reproduce the very high chlorophyll level observed adjacent to the WTP outfall, but this is thought to represent overflow from the WTP pond (Eyre, pers comm). Note that water near the outflow is fresher during July. If adsorption of DIP onto suspended inorganic sediments in the estuary and subsequent settling was the dominant removal mechanism for P, one might expect it to be more effective in July than in September.
River flow was intermediate in April and December, and model-data agreement on TP concentrations and export could only be obtained using half the estimated Mullumbimby WTP P load (Fig. 6.16 and 6.17). Note that both DIP and Chl a are low in April, although TP is comparable to that observed in December. In order to reproduce this effect, it was necessary to assume that much of the load of P from the river and Mullumbimby WTP was effectively refractory. Again, this could be due to binding of DIP to inorganic suspended sediment, or to changes in the composition of organic P.

|
| Figure 6.14. Predicted (line) and observed (diamonds) values of TP, DIP and Chl a, for the Brunswick estuary in September, using a P-limited model with standard parameter values. |
| (original size image) |

|
| Figure 6.15. Predicted (line) and observed (diamonds) values of TP, DIP and Chl a, for the Brunswick estuary in July, using a P-limited model with standard parameter values. |
| (original size image) |
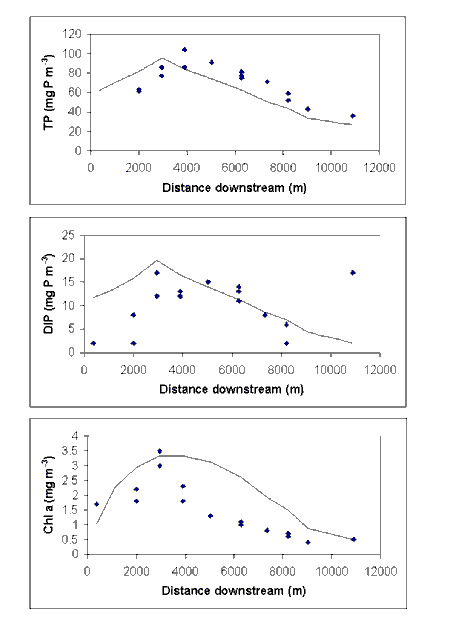
|
| Fig. 6.16. Predicted (line) and observed (diamonds) values of TP, DIP and Chl a, for the Brunswick estuary in April, using a P-limited model with standard parameter values. |
| (original size image) |

|
|
Fig. 6.17. Predicted (line) and observed (diamonds) values of TP, DIP and Chl a, for the Brunswick estuary in December, using a P-limited model with standard parameter values. |
| (original size image) |
The model describes the Brunswick as a P-limited system, which is surprising, given that the N:P ratios of the estimated WTP loads are generally less than Redfield. It appears to be due primarily to the unexplained removal of substantial fractions (50 to 90%) of the estimated TP load from the upstream WTP at Mullumbimby. This could be due to P adsorption and burial in the estuary, but appears likely to be at least partly explained by partial removal of P prior to its discharge into the estuary. Model results suggest that this P removal is critical in reducing algal bloom levels, especially during periods of very low flow.
P-limitation is also increased in the model because phytoplankton require relatively high concentrations of DIP for growth ie KN, the half-saturation constant for P-limited growth, is high. The apparent half-saturation constant may be increased by binding of inorganic P to particles or colloids.
In order to reproduce the observed Chl a and DIP levels, it was necessary to increase the phytoplankton biomass corresponding to maximum grazing mortality, KP. This does not lead to grazing control per se, but does increase grazing losses, and consequently predicted DIP concentrations, under bloom conditions. If this parameter is kept at its original nominal value of 20 mg N m-3 (about 3 mg P or Chl a m-3), the model predicts a large slow-growing phytoplankton biomass with DIP depleted to around 5 to 10 mg P m-3, even for large KN. The large value of KP in the Brunswick estuary may reflect the zooplankton community composition, especially at the fresher end of the estuary where blooms are concentrated. For example, cladocerans are known to have larger values for KP than copepods or microzooplankton (Harris, 1996).
Under the low flow conditions modelled here, the WTPs are the dominant sources of TP and TN (Table 6.4). The Mullumbimby WTP has by far the dominant effect on water quality because its upstream location within the estuary reduces the effective flushing rate. Fig. 6.18 compares predicted chlorophyll and DIN for December for the Mullumbimby discharge in its current location and shifted downstream to the vicinity of the Ocean Shores discharge. Because of the high effective flushing at the latter site, the impact is almost lost within the background gradient, and the dominant influence on estuarine water quality is then the river discharge.
Table 6.4. Range of TN and TP loads (as adjusted in the model) for the low flow periods of April, September and December. | |||
|---|---|---|---|
Source |
TN Load (mg N s-1) |
TP Load (mg P s-1) | |
River |
22 - 66 |
3 - 14 | |
Mullumbimby WTP |
117 |
4 - 18 | |
Ocean Shores WTP |
29 - 36 |
4 19 | |
Brunswick WTP |
58 72 |
19 - 22 | |
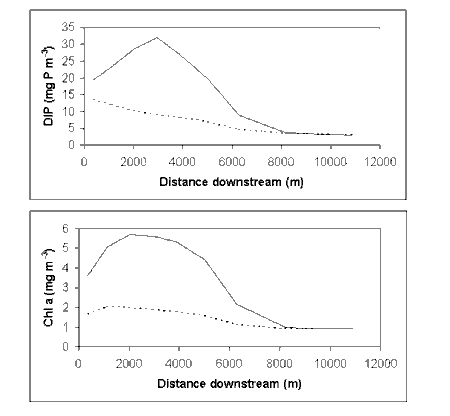
|
| Fig. 6.18. Predicted DIP and Chl a levels for December using the standard parameter set with Mullumbimby discharge located as at present (solid line) and moved to site of Ocean Shores discharge (dashed line). |
| (original size image) |
Hardy Inlet is located in the south-west corner of Western Australia. The inlet is not subject to significant point source loads, and receives diffuse loads of N and P from its main tributaries, the Blackwood and Scott Rivers.
The data used in this test case were acquired in surveys conducted in December 94, August 95 and March 96, by David Deeley, who kindly made them available. A comprehensive suite of physical, chemical and biological variables was measured in the surface and bottom layers at 5 locations along the length of the estuary.
Hardy Inlet is about 11 km from head to mouth, and consists of a broad shallow lagoon, about 3 km across, connected to the ocean by a channel about 500 m wide, with a narrow restricted mouth (Fig. 6.19). Upstream of the lagoon, channels of varying width extend about 4 km to the freshwater sources, the Blackwood River and the Scott River. The broad lagoon and the channel adjacent to the mouth are shallower than 3 m, but there are deeper channels upstream and downstream of the lagoon, with a maximum depth of about 7 m.
There is strong seasonal variation in rainfall and runoff. Flows during summer are typically about 1 m3 s-1 or less, while winter flows reach 100 m3 s-1 for extended periods. The surveys indicate that the estuary is weakly stratified in shallow areas, but can be strongly stratified in the deeper channels in summer and winter.
The inlet is represented here as a two-layer hybrid system, with a surface layer 1 m deep. Partly because of the limited spatial resolution of the surveys, the inlet is divided into 5 columns, each containing one survey station. The lagoon, and the channel upstream of the lagoon, are each represented by one column, with the channel between the lagoon and the ocean divided into three columns.
Salinity data from the three surveys were used to estimate physical exchanges via the inverse technique. The flows corresponding to these surveys were estimated to be 0.67, 88.3 and 0.58 m3 s-1. (There is some uncertainty about the runoff for March 96. Deeley has provided flows for 1995, and on his recommendation, we have assumed the March 1995 flow applies to March 1996, on the basis that summer flows are low and relatively consistent from year to year. The December survey took place on 29 December, 1994, and as early January flows were quite constant, there is likely to be little error in extrapolating these back to 29 December. )

|
|
Fig. 6.19. Hardy Inlet, and sampling sites. |
| (original size image) |
There were some problems in applying the inverse method to the Hardy salinity data. Salinity values in the bottom layer can be much higher in deep holes than in adjacent shallow areas, so that bottom salinity does not decrease monotonically upstream in the bottom layer. The steady-state inverse method is not able to reproduce this behaviour, and it was necessary to adjust bottom salinities so that salinity decreased monotonically upstream in both layers. The largest adjustment was required in August, when residual high salinity water in these deep holes was cut off by overlying fresher water.
The flow in August is sufficiently high to flush the shallower parts of the inlet fresh to the mouth. However, measured salinities are uniformly about 2, rather than zero. We assume this represents the salinity of runoff from the catchment.
The upstream station in the estuary did not sample fresh water (except in August), so we could not estimate loads by multiplying upstream concentrations by flows. Time series of estimated daily loads of DIN, TN, DIP and TP for 1995 were provided by David Deeley. Loads averaged over the 5 days preceding each survey were used to drive the steady-state model simulation. Organic N and P loads were assumed to be refractory (see below).
Observed concentrations of DIN, DIP, TN and TP at the station near the mouth of the estuary were used as a marine boundary condition. Again, the measured organic N was assumed to be predominantly or entirely refractory (see below).
It is possible to model Hardy Inlet as an N-limited system. Fig. 6.20 compares predicted and observed TN, DIN, and Chl a in the surface layer in December 1994, using a standard parameter set identical to that used for the Derwent (Table 6.2), except that the half-saturation constant for growth, KN, has been increased from 10 to 20 mg N m-3. A value of K0 = 1 m-1 is adopted for the Hardy, based on observed Secchi depths of about 2 m.
The model reproduces the observed distributions in December 1994 quite well, although it over-estimates Chl a and underestimates DIN in the middle estuary. The model also reproduces DIN and Chl a well in the bottom layer. A similar result is obtained using the same parameter set for March 1996. The model reproduces the observed chlorophyll levels in March very well, but again underestimates the observed DIN levels (Fig. 6.21).
The December and March surveys were conducted in summer under conditions of low flow and weak flushing, when the inlet is strongly marine in character. By contrast, August is a period of high flow and strong flushing, when salinities are uniformly low throughout the inlet. Here, concentrations of TN, DIN and Chl a in the surface layer are dominated by the inflow concentrations. While DIN concentrations are very high, the rapid flushing allows only a weak response from phytoplankton growth within the inlet (Fig. 6.22).
Denitrification is switched on in these runs, and might be expected to make a significant contribution to the N budget at least in summer, under conditions of low flow and long flushing times. Fig. 6.23 shows the effect of switching off denitrification in March 1996. While this does not strongly affect the overall TN budget, which is dominated by exchanges of refractory organic N, it does increase the pool of "available" N, which appears as a doubling in Chl a.
While the N-based model predicts the observed chlorophyll values reasonably well, it does so using a rather high value for the half-saturation constant for N-limited growth, and then still underpredicts DIN levels in summer. This suggests that N may not be limiting, especially given that the observed DIP values in the Hardy are very low. As in the case of the Brunswick, we have implemented a simple P-limited model of Hardy Inlet.

|
| Fig. 6.20. Observed (diamonds) and predicted (open squares) distribution of TN, DIN and Chl a for Hardy Inlet in December 94. |
| (original size image) |

|
| Fig. 6.21. Observed (diamonds) and predicted (open squares) distribution of TN, DIN and Chl a for Hardy Inlet in March 96. |
| (original size image) |

|
|
Fig. 6.22. Predicted (diamonds) and observed (open squares) distribution of TN, DIN and Chl a for Hardy Inlet in August 95. |
| (original size image) |

|
|
Fig. 6.23. Comparison of predicted TN, DIN and Chl a in the surface layer in Hardy Inlet in March 1996 for standard parameters (open squares) and with denitrification switched off (diamonds). |
| (original size image) |
The standard parameter set used to model the Hardy as a P-limited system is given in Table 6.5. There are certain key changes from those used to model the Brunswick estuary. The maximum phytoplankton growth rate is reduced to 1.5 d-1. More importantly, the half-saturation constant for DIP-limited growth is reduced to low values, 1 to 10 mg P m-3. KP is left at a standard P-equivalent value of 3 mg P m-3. However, the recycling efficiency of P in the water column has been reduced substantially by increasing both fDET (the fraction of phytoplankton losses directed to organic P as opposed to DIP), and fREF (the fraction of labile organic P directed to refractory organic P). The reasons for these changes are discussed below.
Table 6.5. "Standard" parameter set used in Hardy P-limited simulations (see text). | |||
|---|---|---|---|
Symbol |
Description |
Units |
Value |
mmax |
Maximum phytoplankton growth rate |
d-1 |
1.5 |
KN |
Half-saturation constant for phytoplankton growth on DIN |
mg P m-3 |
1 to 10 |
IK |
Light saturation intensity |
W m-2 |
10 |
m0 |
Background constant phytoplankton loss rate |
d-1 |
0.1 |
m1 |
Maximum grazing loss rate |
d-1 |
0.6 |
KP |
Phytoplankton biomass corresponding to maximum grazing loss rate |
mg P m-3 |
3 |
fDET |
Fraction of grazing losses to labile detritus |
0.7 | |
fREF |
Fraction of labile detritus to refractory detritus |
0.5 | |
rDET |
Breakdown rate of labile detritus |
d-1 |
0.1 |
rREF |
Breakdown rate of refractory detritus |
d-1 |
0.01 |
EDENmax |
Maximum denitrification efficiency |
0 | |
R0 |
Sediment respiration rate at which EDEN = 0. |
mg N m-2 d-1 |
NA |
K0 |
Background light attenuation |
m-1 |
2.0 |
k*PHY |
Specific light attenuation for phytoplankton |
m2 (mg P)-1 |
0.02 |
k*DET |
Specific light attenuation for labile detritus. |
m2 (mg P)-1 |
0.02 |
k*REF |
Specific light attenuation for refractory organic N |
m2 (mg P)-1 |
0.006 |
wPHY |
Sinking rate of phytoplankton |
m d-1 |
0 |
wDET |
Sinking rate of labile detritus |
m d-1 |
0 |
wREF |
Sinking rate of refractory organic N |
m d-1 |
0 |
In December and March, the model reproduces well the observed levels of DIP, and of Chl a in March, although it overestimates Chl a by about a factor of 2 in December (Fig. 6.24 and 6.25). The model reproduces the very low DIP levels observed in March, but only by adopting a low value of 1 mg P m-3 for KN.
The TP loads in December and March are 40 to 50% DIP, and these could potentially support much higher levels of Chl a. The DIP is drawn down to low levels, but P is present in the water column primarily as non-phytoplankton organic P. The model is only capable of simulating this if a high proportion of phytoplankton losses is directed to organic detritus, and ultimately to refractory organic P. The high observed levels of TP are consistent with export of most or all of the estimated loads, suggesting that P burial in sediments is not a major sink.
In fact, although it conserves total P, the model underestimates surface layer TP concentrations and export in March (Fig. 6.25). This suggests there is a missing source rather than sink of P in March. For the estimated physical exchanges, the model can only match the observed TP concentrations (and implicitly P export), if there is an additional load of refractory organic P into the inlet which is about 10 times the estimated organic P load from the catchment. The loads in March 1996 are unknown and have been assumed equal to the estimated loads for March 1995. It is possible that this assumption is incorrect, and that runoff and loads were significantly higher in March 1996.

|
|
Fig. 6.24. Comparison of observed (diamonds) and predicted (open squares) concentrations of TP, DIP and Chl a, in surface and bottom layers, for Hardy Inlet in December 1994. |
| (original size image) |

|
|
Fig. 6.25. Comparison of observed (diamonds) and predicted (open squares) concentrations of TP, DIP and Chl a, in surface and bottom layers, for Hardy Inlet in March 1996. |
| (original size image) |
The model generally reproduces well the observed TP, DIP and Chl a distributions in August 1995 (Fig. 6.26), although it is not capable of reproducing the anomalous TP and Chla values observed in deep bottom layers containing isolated high salinity water. In the surface layers, the predicted concentrations are almost entirely independent of biogeochemical parameters, and are determined by the concentrations in the inflow. However, it was necessary to increase the organic P load again, this time by a factor of 5, to match the observed concentrations in the inlet. This suggests that the estimates of catchment load provided may systematically underestimate organic P loads.
Given the extremely low levels of DIP observed in March 1996, it seems clear that the Hardy was P-limited at that time, and likely that it was operating as a P-limited system in December 1994. However, unlike the Brunswick, DIN does not accumulate to very high levels, and N and P appear to be in close balance, presumably reflecting the balance in diffuse loads. Unlike the Brunswick, there is no evidence for an unidentified P sink; instead, there seems to be an unidentified P source.
The fact that the observed chlorophyll levels can be predicted with an N-based model (albeit with rather high values of KN), points to the risk that models can make correct predictions for the wrong reasons.

|
|
Fig. 6.26. Comparison of observed (diamonds) and predicted (open squares) concentrations of TP, DIP and Chl a, in surface and bottom layers, for Hardy Inlet in August 1995. |
| (original size image) |
The choice of test cases in this study has depended primarily on the availability of suitable data sets, and no conclusions about relative frequency should be drawn from the fact that two of the 3 estuaries chosen have turned out to be P-limited. However, this does highlight the ambiguous position of estuaries with regard to limiting nutrients. It is clearly desirable to extend the simple model applied here to incorporate simultaneous N and P limitation.
Physically, the test cases have included a deep, salt-wedge estuary, a well-mixed tidally dominated estuary, and an enclosed inlet with variable stratification. The salinity-based inverse approach to transport modelling has worked well in all three cases. It has the particular advantage that it allows us to be confident that the model physical exchanges are consistent with the observed distribution of a conserved tracer (salt), and therefore prediction errors for other biogeochemical variables reflect unidentified sources or sinks. In this sense, it represents a more sophisticated version of the traditional mixing curve. We have been able to use this in all three test cases to identify unexplained sources or sinks of nitrogen or phosphorous. In other words, simple models of N or P cycling based on the inverse model are particularly useful for diagnostic as well as prognostic purposes.
Aside from the question of N or P limitation, the test cases also serve to highlight the variation among estuaries in the interaction of physical exchanges or flushing, nutrient loads and cycling, and light attenuation, in controlling phytoplankton biomass. Light attenuation plays a critical role in the Derwent but not in the Brunswick, which although more turbid is much shallower. Effective flushing rates increase towards the mouths of estuaries, and in both the Derwent and Brunswick, the impact of point sources on chlorophyll levels depends critically on their location along the estuary. This effect may be exacerbated in salt-wedge estuaries such as the Derwent if effluent is discharged into the lower layer where it is carried further upstream. Seasonal changes in growth and mortality rates, presumably driven by temperature, appear to play a critical role in the Derwent, but not in the Brunswick or Hardy. It is quite straightforward to include temperature dependence of growth rates in the model.
These results suggest that a simple model can encapsulate the key processes controlling phytoplankton biomass and nutrient concentrations in a wide range of estuaries. However, this model cannot be applied "blindly" with fixed parameter values. While some parameter values were robust (or at least model predictions were not sensitive to their value across these applications), it was necessary to make changes in other parameter values in order to reproduce observations in the test cases selected. Application of the model to a broader range of test cases will be necessary before we can generalise about the stability or otherwise of these parameters.
Algal bloom composition is of interest to environmental managers for several reasons. Some bloom species are known to produce toxins, which can cause mass mortality of marine biota, including farmed species, or represent a health risk to humans, requiring for example closure of shellfish farms. Toxic species occur commonly among the dinoflagellates, but toxins have also been identified in diatoms and other phytoplankton classes.
Bloom composition is also potentially important because it can feed back to affect nutrient cycling and bloom dynamics. Nitrogen-fixing cyanobacteria, for example, can produce dense blooms when N is limiting and P is abundant. Other taxa have specific nutrient requirements: for example, diatoms require silicate. Some dinoflagellates are known to undergo diel vertical migration, taking up nutrients from bottom water at night, and moving to the surface to photosynthesize during the day. Eco-physiological parameters such as maximum phytoplankton growth rates, half-saturation constants for light and nutrient limitation, and grazing loss rates, also vary with composition.
A workshop on algal bloom composition was held in Hobart on 4 August 1997, attended by Sue Blackburn, Scott Condie, Graham Harris, Ian Jameson, Malcolm McCausland, Sandy Murray, Naomi Parker, John Parslow, Peter Thompson, and Stephen Walker. The workshop considered the factors affecting bloom composition, our ability to predict bloom composition, and the likely feedbacks on eutrophication and prediction of algal biomass. The following relies heavily on the outcomes of the workshop, and the contribution of participants is gratefully acknowledged.
Prediction of bloom composition at the level of individual species seems unlikely to be successful, and it is more appropriate to concentrate on the identification and prediction of functional classes of algae. The following functional groups are proposed as a first, coarse-level classification. Macrophytes, including macroalgae and seagrasses, are included because of their potential interaction with phytoplankton blooms in shallow systems.
Bloom phytoplankton species, divided into:
There are two ways to predict bloom composition at this functional level. One is to include the functional groups as explicit state variables in a dynamical model, and try to predict relative abundance as an outcome of competition for light, nutrients, etc. This requires the development of complex dynamical models with many state variables and parameters (discussed in Chapter 3). There has been some success with this approach in both freshwater and marine systems (Murray and Parslow, 1997).
A second approach is to use simple dynamical models to predict algal biomass, and then use empirical models or qualitative rules to predict the probable bloom composition based on environmental factors. The workshop developed a table linking phytoplankton bloom composition to requirements/tolerances for a set of 9 environmental factors (Table 7.1). Entries in the table at this stage are based on the experience of the participants, and/or known differences in the autecology of different functional groups. Lack of knowledge for a given combination is indicated by a question mark.
| Table 7.1. Requirements of functional groups across 9 environmental factors. | ||||||
|---|---|---|---|---|---|---|
Factor |
Small cells |
Dino- flagellate |
Freshwater cyano-bacteria |
Brackish cyano-bacteria |
Diatoms |
Euglenoids |
Organics |
some spp |
Humics |
none |
? |
none |
high |
Salinity |
variable |
variable |
<10 |
<25-30 |
variable |
low |
Si |
none |
none |
none |
none |
high |
none |
N |
low |
high |
low |
low |
low |
? |
P |
low |
high |
high |
high |
low |
high |
Stratification |
variable |
high |
high |
variable |
low |
? |
Light |
mod-high |
high |
high |
high |
low |
low |
Flushing |
high |
low |
low |
low |
high |
low |
Temperature |
high |
variable |
high |
cool |
variable |
warm |
A number of the environmental factors deserve further comment.
The organic concentrations or loads in row 1 represent labile organics of the kind introduced by STP overflows. There is evidence that dinoflagellate blooms are associated with high loads of refractory dissolved organics (humics). It is not clear whether these have a direct or indirect effect on dinoflagellate growth.
The nutrient requirements could in principle refer to concentrations or supply rates (internal loads). Under oligotrophic conditions, where concentrations are very low, internal loads may be more appropriate, but harder to measure. Internal loads could be predicted by a biomass model.
Dinoflagellates are thought to be favoured by persistent stratification associated with high light attenuation, so that the water column is separated into an upper nutrient-limited layer and a lower light-limited layer. Dinoflagellates then migrate vertically to exploit both. The frequency and duration of stratification is clearly important. Mixed dinoflagellate / diatom blooms may be favoured by intermittent stratification.
For phytoplankton, light refers to the mean PAR in the water column, or in the surface layer in stratified systems. For benthic macrophytes, light refers to bottom light intensities. For high values of the light attenuation coefficient K or large depths H, depth averaged light intensity falls off like 1/(K.H), whereas bottom light falls off like exp(-K.H), so that macrophytes are much more sensitive to increasing light attenuation. Under conditions of weak mixing, motile or buoyant species may be able to maximize light availability by staying in the surface layer during daylight.
The significance of other environmental factors is still under investigation. Micronutrients (especially iron) are now thought to limit phytoplankton biomass over large ocean areas. Although levels of total iron are much higher in coastal waters, iron chemistry is complex and its bio-availability is unclear.
N-fixing cyanobacteria have been divided into "fresh-water" species which may survive in the upper estuary, and brackish species (Nodularia) which appear to thrive at salinities below about 30. One of the (fortunate) anomalies in coastal waters has been the absence of N-fixing cyanobacteria at full marine salinities. However, studies in Moreton Bay have recently found extensive blooms of the benthic N-fixing cyanobacteria, Lyngbya. These occur in association with high levels of iron released from acid-sulphate soils, and Dennison (pers. comm.) has suggested that this species, and perhaps other marine nitrogen fixers, may have high iron requirements.
This table can be used "as is" as a qualitative guide to dominance, and to derive certain simple rules of thumb. Thus, in a well-mixed water column, with high levels of N, P and silicate, diatoms are likely to dominate. In well-stratified waters with high light attenuation, and build-up of nutrients in bottom waters, dinoflagellates are able to dominate by virtue of their ability to vertically migrate. Such situations are common in estuaries in southern Australia subject to moderate runoff with high humic levels. In oligotrophic waters, small flagellates are usually present at persistent low concentrations, with diatoms responding rapidly to episodic nutrient injections. Shallow systems with low nutrient levels and high light penetration favour seagrasses, while shallow systems with high nutrient concentrations and stable sediments favour green macro-algae such as Ulva. Filamentous drift algae appear to accumulate in quite deep waters in embayments such as Jervis Bay and Port Phillip Bay.
Given a large set of observations of algal composition and associated environmental factors, one could attempt to develop and calibrate a more formal predictive model. Formal models could be probabilistic, or based on new empirical approaches such as fuzzy logic or neural networks. Models of this kind are currently being developed to predict bloom composition based on time series of observations from individual estuaries. As further data sets and experience are acquired, it may be possible to integrate these modelling attempts into a more general framework.
Most of the parameters and process formulations in biomass models (eg maximum growth rates) depend on algal composition.
Oligotrophic plankton communities are dominated by small phytoplankton which have high specific growth rates and loss rates even at quite low ambient nutrient concentrations. These small phytoplankton (picophytoplankton and small nano-flagellates) respond only weakly when nutrients are added. This has been attributed to grazing control by rapidly growing zooflagellates and microzooplankton, which are capable of exerting water column clearance rates exceeding phytoplankton maximum growth rates. Bloom phytoplankton such as diatoms, dinoflagellates and blue-green algae are generally subject to lower grazing rates. Specific grazing loss rates seem likely to decrease at high biomass levels (ie under bloom conditions) as larger zooplankton are saturated.
The parameters and even the behaviour of phytoplankton mortality as a function of biomass may therefore shift depending on which functional group is represented. A generic model should arguably try to incorporate the effects of changes in composition as biomass increases.
Decline of phytoplankton blooms can be due to grazing, to settling out, or other sources of mortality (cell lysis, bacterial or viral attack) associated with nutrient depletion and cell senescence. There is evidence for enhanced sinking rates by marine diatoms following nutient depletion.
While diatoms are capable of very high specific growth rates, many dinoflagellates and some blue-greens have quite low maximum growth rates. These organisms can only bloom under prolonged favourable conditions with low combined loss rates.
Macrophytes have relatively slow specific growth rates and are subject to shading. However, they may be favoured in shallow lagoons, especially if phytoplankton are subject to high or episodic flushing.
The N-fixing blue-green Nodularia has a low maximum growth rate, and Nodularia blooms generally occur in quite shallow systems (<3m depth) with low flushing rates.
Nitrogen fixation in sediments can be enhanced in seagrass beds, and can represent an important contribution to the N load in oligotrophic shallow systems with widespread seagrass communities, such as Moreton Bay. This is less likely to be important in mesotrophic or eutrophic estuaries.
The feedback effects of bloom composition could be represented explicitly in eutrophication models in one of two ways. One could in principle develop an interative procedure, in which algal biomass and nutrient levels are predicted, then bloom composition is predicted, and the dynamical model parameters are adjusted according to the bloom composition. However, if one had parameter sets appropriate to different functional groups, it could be argued that one might just as well develop a more complex dynamical model incorporating multiple functional groups explicitly. Again, further experience with application of models to a wide range of systems is required to choose between these approaches.
The objective of this study has been "to develop and demonstrate a widely applicable model of eutrophication processes in urban estuaries which can predict the potential for phytoplankton blooms and bloom type on the basis of environmental data". Existing estuarine eutrophication models range from simple load-response relationships to complex "realistic" process-based simulation models. After reviewing these models in Chapters 1 to 3, we decided to focus on the development of relatively simple process-based models, which incorporate the core variables and processes controlling the cycling of nutrients and bloom development in estuaries. We argued that models of this kind should offer advantages over load-response models in dealing with the wide range of physical environmental conditions in estuaries, and offer advantages over more complex models in reduced data requirements, lower implementation costs, and amenability to analysis and understanding.
We have in fact developed two models, which share essentially the same state variables and underlying biogeochemical process formulation, but differ in their physical formulation. The first (Chapter 4) is developed as a steady-state one-box model, and can be regarded as a direct process-based analogue of the load-response models. The second (Chapter 6) is developed as a spatially-resolved dynamical model, with an underlying physical transport model based on an inverse modelling technique. Both models were developed as nitrogen-based models, although the second has been adapted as a P-based model.
The steady-state one-box model can be solved to obtain explicit relationships between the model state variables and nitrogen loads. By analogy with the Vollenweider load-response models, we can think of this model as defining two kinds of relationships:
The relationship between TN load and TN pool is determined by a combination of flushing and internal sinks. In the absence of an internal sink, the TN pool is proportional to load multiplied by flushing time. However, flushing rates in estuaries are determined by a combination of freshwater inflow and exchange with the ocean driven by tidal and wind mixing. Under steady-state assumptions, flushing rates can be inferred from salinity balance.
Analysis of the one-box model (Chapter 4) suggests that denitrification is likely to be an important internal sink for estuaries with relatively long flushing times, of order 100 days. In these estuaries, denitrification may account for most of the (labile) nitrogen load, and maintain the estuary in a mesotrophic state under loads which would otherwise create eutrophic conditions. Estuaries of this type are then subject to catastrophic failure, if loads and the consequent organic flux to the sediment increase sufficiently to cause sediment denitrification to shut down (Murray and Parslow, 1997). Results from Port Phillip Bay suggest a critical nitrogen load of about 30 mg N m-2 d-1. Coastal lagoons are common along parts of the Australian coastline, and these usually have restricted entrances which may even close for long periods under low flow conditions. These lagoons are likely to be especially vulnerable to denitrification failure.
In estuaries with short flushing times (order 10 days), denitrification accounts for a minority of the nitrogen load. These systems are not subject to catastrophic failure, but undergo a smooth transition from mesotrophic to eutrophic state as loads increase.
Flushing rates also interact with sediment resuspension rates and detrital remineralization rates to determine the proportion of labile and refractory detritus remineralised in the estuary. In estuaries with flushing times of order 100 days, refractory detritus accumulates in sediments and plays a significant role in nitrogen cycling. In estuaries with short flushing times, refractory detritus plays little active role in the nitrogen cycle, and may act as a conservative tracer. (However, it should be remembered that we have little quantitative knowledge of the chemical composition of refractory organic N, and of the factors controlling its remineralization.)
The composition of the TN pool is strongly affected by the light environment in estuaries. In estuaries which have low background light attenuation, phytoplankton biomass and associated products are the dominant control on light attenuation. As loads of DIN into these estuaries increase, phytoplankton maintain DIN at low levels until phytoplankton biomass builds up to very high levels (order 20 - 50 mg Chl a m-3) where self-shading limits growth and DIN uptake. Further increases in load result in accumulation of DIN. In deep estuaries which have high background light attenuation due either to turbidity or high levels of humics in runoff, light limitation can restrict phytoplankton biomass to quite low levels (order 2 - 5 mg Chl a m-3), and excess DIN will accumulate even at low loads.
Low light intensities and high DIN levels may favour a different denitrification pathway, in which nitrification takes place in the water column, and the resulting nitrate diffuses into the sediment where it is denitrified. The resulting sink can affect the mass balance of N and its delivery to adjacent coastal waters, but is unlikely to significantly modify water quality in the estuary itself.
A complication affecting both the prediction and interpretation of TN composition is the presence of high levels of refractory organic N. It seems likely that in most estuaries this refractory organic N is derived both from the catchment and from exchange with coastal marine waters. At low to moderate loads (oligotrophic to mesotrophic conditions), this material can dominate the TN pool. It is important that this material, and particularly the ocean boundary concentrations, be taken into account in constructing mass balances. The lack of operational methods to distinguish labile and refractory organic N in catchment loads and coastal waters creates considerable uncertainty about the fate and "availability" of loads, and tends to confound mass balance in estuaries.
The one-box model offers considerable insight into the processes controlling N cycling and phytoplankton biomass, and may provide quite a reasonable representation of coastal embayments and lagoons with restricted entrances in which internal mixing times are short compared with flushing times. However, the one-box model cannot represent more "classical" estuaries with large along-estuary salinity gradients. For these estuaries, the concept of a single flushing time is simply not valid, and a spatially-resolved model is required.
The traditional approach to developing spatially-resolved models of coastal marine systems has been to build a hydrodynamic model, and then derive a transport model for biogeochemical tracers. However, unless the hydrodynamic model has very high spatial resolution in the horizontal and the vertical, it will not be able to resolve the effects of fine-scale bathymetry and density gradients which control mixing in estuaries. Simpler 1-D or 2-D "vertical slice" hydrodynamic models may reproduce tidal height and currents quite well, but not reproduce mixing and salinity distributions unless these are heavily parameterised. The approach adopted here has been to forego the hydrodynamic model and use inverse models to infer the exchanges from the observed salinity distribution.
This approach can be regarded as an extension of more traditional methods which use the salinity distribution to infer flushing rates. The key limitation is the assumption of steady-state flow and exchanges. As discussed in Chapter 5, this assumption is reasonable provided river flow changes on time scales which are not too short compared with flushing times. Many Australian estuaries are subject to long periods of low flow, with intermittent flood events. The steady-state assumption works quite well during the low-flow periods, but is likely to fail during brief flood events. In those urban estuaries where point source loads are the major cause of eutrophication, water quality problems are most apparent during low-flow periods, and modelling these may be sufficient. Where diffuse loads dominate, or the interaction between diffuse and point source loads is thought to be critical, more sophisticated dynamical models may be required.
The spatially resolved biogeochemical model (SEEM) has been implemented as a dynamical model, but the applications to date have been steady-state. The test cases addressed in Chapter 6 cover three estuaries which represent very different environments in terms of morphology, runoff, stratification, and light attenuation. These test cases reinforce some of the conclusions from the one-box model analysis, but also raise new issues.
The most striking feature of the test cases is the importance of P limitation in the Brunswick and Hardy Inlet, and the need to address N and P limitation. We concentrated on N-limited models in the expectation that these would apply to most estuaries. This may still be true: after all, 3 is a small sample size. However, these test cases do provide some insight into the factors affecting N and P limitation. The Derwent River contains almost zero DIP and moderate concentrations of DIN, and the freshwater end of the estuary is P-limited. The middle and lower Derwent is dominated (at least in summer) by secondary-treated effluent, which has N:P ratios below Redfield, and tends to drive the estuary into N limitation. In the case of the Derwent, this appears to be exacerbated by N removal in the upper estuary, possibly due to denitrification. In winter, the Derwent receives large DIN and DIP loads from the adjacent continental shelf, where elevated concentrations of nutrients result from winter mixing. These loads will also be balanced in favour of N limitation.
The Brunswick appears to be P-limited. It is dominated by the Mullumbimby WTP load in the upper estuary, and we are unable to conclude from the available data whether the P-limitation is due to sequestration of the nominal WTP P load before or after it reaches the estuary, although we suspect the former. P-removal is often the first step in tertiary treatment, and where this is applied without N-removal, it is likely to drive estuaries into P-limitation.
Hardy Inlet is interesting because it receives catchment loads which appear to be fairly close to Redfield balance, but slightly favour P-limitation. The fact that DIP is depleted in the estuary suggests that denitrification is not important, despite low to moderate flushing rates.
The use of the inverse transport model allows us to diagnose internal sinks through a failure in mass-balance of TN or TP. However, this is complicated by the presence in all three test cases of high levels of organic N and P, which tend to dominate the mass balance, especially in the case of N. These are driven by loads of refractory organic matter from both catchment and ocean. The problem is that internal sinks may be an appreciable part of the "available" N budget, but a small part of the total N budget.
The test cases again highlight the importance of light attenuation and depth in controlling phytoplankton biomass and utilisation of DIN/DIP. The Derwent and Brunswick provide an interesting contrast in the interplay between light attenuation and depth. The Derwent has moderate light attenuation but is deep, and phytoplankton are strongly light-limited, especially in winter. The Brunswick has very high light attenuation but is shallow, and can support high phytoplankton biomass. At least in the Derwent, there is evidence that seasonal changes in light and temperature also control DIN utilisation through their effect on phytoplankton growth rates.
The Derwent and Brunswick test cases highlight the critical importance of the location of point source discharges. Effective flushing rates can vary by more than an order of magnitude along estuary. In the case of the Derwent, shifting an outfall by 10 km in the mid-estuary has a major impact on resulting water quality. In strongly stratified salt-wedge estuaries, the location in the vertical is also important. The two-layer circulation combined with sinking can act to trap particles in the estuary, and discharging effluent into bottom waters can greatly increase residence time and water quality impacts.
A key advantage of simpler models is their reduced data requirement. The models presented here have been designed to be calibrated using data collected on more or less "routine" environmental surveys. We offer here guidelines for the design of these surveys.
The model has been implemented in a modular way that allows new state variables and/or processes to be added easily. Some priorities for futher enhancement have emerged from the test cases.
It is easy to come up with justifications for adding other state variables and processes to the model. However, this will quickly lead back to models of the complexity of the Port Phillip Bay Integrated Model, or ERSEM. If the advantages of simple models are not to be lost, additional state variables and processes should only be added as it is established that these are essential for adequate model performance in a substantial fraction of estuaries.
Arguably, the most important priority for future development is not elaborating or refining the model, but building a robust statistically rigorous parameter estimation framework around the model. In the test cases presented here, the model has been fitted subjectively to the observations. In most cases, it has only been necessary to modify a small subset of the parameters, but selecting this subset requires a good understanding of the model behaviour and its dependence on parameter values, and of the a priori constraints on parameter values. This means that applications of the model still require "expert" input. It also means that we have no formal measure either of the goodness of fit using the selected parameters, nor any assessment of the region in parameter space which would give equivalent model performance.
There are a range of formal parameter estimation procedures which could be used to fit the SEEM model to observations. The more sophisticated Bayesian techniques, such as the Monte Carlo Markov Chain method (Harmon and Challenor, 1997), allow the user to establish prior probability distributions for the parameters, and provide a complete characterisation of their joint posterior probability distribution. These methods can be used not only to quantify the uncertainty in management predictions, but also to quantitatively assess the information content provided by alternative field measurement programs. These methods are very computationally intensive, but should be feasible for models of the degree of complexity considered here.
We see the development of a parameter estimation framework of this kind around SEEM, and the application of the combined package to a much broader range of estuaries, as the logical next step.
(In order of appearance)
Symbol |
Units |
Description |
t |
d |
Flushing time. |
R |
m3 d-1 |
River or freshwater flow. |
r |
d-1 |
Flushing rate |
V |
m3 |
Lake / estuary volume |
M |
mg m-3 |
Concentration of generic tracer "M" |
LM |
mg M d-1 |
Total load of tracer M |
LM |
mg M m-3 d-1 |
Load of tracer M per unit volume (= LM/V). |
TP |
mg P m-3 |
Total Phosphorous |
S |
mg P d-1 |
Total internal sink of TP. |
w |
m d-1 |
Effective "sedimentation rate" of TP. |
DIN |
mg N m-3 |
Dissolved inorganic nitrogen |
PHY |
mg N m-3 |
Phytoplankton concentration (nitrogen) |
DET |
mg N m-3 |
Labile detrital nitrogen. |
ZOO |
mg N m-3 |
Zooplankton biomass as nitrogen. |
m |
d-1 |
Phytoplankton growth rate |
m max |
d-1 |
Maximum phytoplankton growth rate. |
hN |
Growth limitation factor due to nutrient. |
|
hI |
Growth limitation factor due to light. |
|
KN |
mg N m-3 |
Half-saturation constant for growth. |
IK |
W m-2 |
Saturation light intensity |
I0 |
W m-2 |
Surface light intensity |
K |
m-1 |
Diffuse light attenuation |
H |
m |
Depth |
<I> |
W m-2 |
Average water-column light intensity. |
K0 |
m-1 |
Background light attenuation. |
k*X |
m2 (mg X)-1 |
Specific light attenuation for constituent X. |
G |
d-1 |
Phytoplankton N consumed per unit zooplankton N per day. |
Gmax |
d-1 |
Maximum phytoplankton N consumed per unit zooplankton N per day. |
KP |
mg N m-3 |
Half-saturation constant for zooplankton grazing on phytoplankton. |
PHY0 |
mg N m-3 |
Threshold phytoplankton biomass for grazing. |
EZ |
Zooplankton gross growth efficiency. |
|
mQ |
d-1 (mg N m-3)-1 |
Zooplankton quadratic mortality cooefficient. |
rDET |
d-1 |
Remineralization rate of labile detritus. |
EDEN |
Denitrification efficiency. |
|
EDENmax |
Maximum denitrification efficiency. |
|
RSED |
mg N m-3 d-1 |
Sediment respiration rate / depth. |
R0 |
mg N m-3 d-1 |
Value of RSED at which EDEN =0. |
R0* |
mg N m-2 d-1 |
Sediment respiration rate (ie per unit area) at which EDEN =0. |
s X |
Fraction of constituent X suspended in water column. |
|
REF |
mg N m-3 |
Refractory detrital N |
fDET |
Fraction of phytoplankton losses assigned to labile detritus. |
|
m |
d-1 |
Phytoplankton loss rate |
rREF |
d-1 |
Remineralization rate of refractory detritus. |
fREF |
Fraction of labile detritus converted to refractory detritus. |
|
XO |
mg N m-3 |
Ocean concentration of constituent X. |
m0 |
d-1 |
Base phytoplankton loss rate. |
m1 |
d-1 |
Maximum phytoplankton loss rate due to grazing. |
TN |
mg N m-3 |
Total nitrogen concentration |
TNW |
mg N m-3 |
Concentration of total nitrogen suspended in water column. |
TN* |
mg N m-3 |
Value of TNW for export to balance loads |
DETI |
mg N m-3 |
Concentration of labile detritus produced internally. |
REFI |
mg N m-3 |
Concentration of refractory detritus produced internally. |
hN* |
Nutrient-limited growth reduction factor required for phytoplankton growth to balance losses. |
|
L*(PHY) |
mg N m-3 d-1 |
DIN load required to balance losses at phytoplankton concentration PHY. |
Us |
m s-1 |
Surface current |
Uf |
m s-1 |
Sectionally-averaged current. |
d S |
Top-to-bottom salinity difference. |
|
SO |
Sectionally-averaged salinity. |
|
n |
Diffusive fraction. |
|
qi,i+1 |
m3 s-1 |
Horizontal volume flux from cell i to i+1. |
Ci |
mg C m-3 |
Concentration of tracer C in cell i. |
Si |
Salinity in cell i. |
|
Qi |
mg C m-3 s-1 |
Source of tracer C in cell i. |
Ciu, Cil |
mg C m-3 |
Concentration of tracer C in column i, and upper or lower cell respectively. |
qi+, qi- |
m3 s-1 |
Volume flux in column i from lower to upper, and upper to lower cell respectively. |
qi,i+1u, qi,i+1l |
m3 s-1 |
Volume flux from column i to i+1 in upper and lower layers respectively. |
Cij |
mg C m-3 |
Concentration of tracer C in column i, layer j. |
qij,j+1 |
m3 s-1 |
Volume flux in column i from layer j to j+1 |
qi,i+1j |
m3 s-1 |
Volume flux in layer j from column i to i+1. |
Qij |
mg C m-3 s-1 |
Source of tracer C in column i, layer j. |
SVD |
Singular value decomposition. |
|
wj |
Weight assigned to layer j in computing diffusive fraction. |
|
T |
m3 s-1 |
Flow component due to river flow. |
A |
m3 s-1 |
Remaining advective flow component. |
D |
m3 s-1 |
Diffusive component of fluxes. |
d |
m3 s-1 |
Flux correction for upstream differencing |
Qkl |
m3 s-1 |
Vector of fluxes associated with river flow l. |
zk |
m |
Height of top of layer k. |
Hk |
m |
Thickness of layer k. |
<I>k |
W m-2 |
Mean light intensity in layer k. |
Su |
d-1 |
Resuspension rate in layer k |
wX |
m d-1 |
Sinking rate of constituent X. |
Ak |
m2 |
Area of top of layer k |
 Riversinfo Australia (au.riversinfo.org): Publication Information:
Riversinfo Australia (au.riversinfo.org): Publication Information:
Current at December 2002
 au.riversinfo.org has been developed to facilitate public access to scientific and technical information on Australia's Rivers. Much of this material was paid for using public funds and is therefore owned by the Australian people. Environment Australia have been instrumental in making available all the publications from:
au.riversinfo.org has been developed to facilitate public access to scientific and technical information on Australia's Rivers. Much of this material was paid for using public funds and is therefore owned by the Australian people. Environment Australia have been instrumental in making available all the publications from:
 The au.riversinfo.org Internet site is in-part supported by the Natural Heritage Trust. The Natural Heritage Trust focuses on five key environmental themes - land, vegetation, rivers, coasts and marine, and biodiversity. The programs of the Natural Heritage Trust play a major role in developing sustainable agriculture and natural resource management, as well as protecting our unique biodiversity through improved management and delivery of resources.
The au.riversinfo.org Internet site is in-part supported by the Natural Heritage Trust. The Natural Heritage Trust focuses on five key environmental themes - land, vegetation, rivers, coasts and marine, and biodiversity. The programs of the Natural Heritage Trust play a major role in developing sustainable agriculture and natural resource management, as well as protecting our unique biodiversity through improved management and delivery of resources.
 The au.riversinfo.org Internet site is in-part supported by Sydney Airport who have co-funded a Natural Heritage Trust supported project intended to develop Internet based environmental information integration and management systems. This will assist in developing an overall perspective on the demands and uses for environmental resources
The au.riversinfo.org Internet site is in-part supported by Sydney Airport who have co-funded a Natural Heritage Trust supported project intended to develop Internet based environmental information integration and management systems. This will assist in developing an overall perspective on the demands and uses for environmental resources